Идеальная планировка города. Продолжение темы.
В прошлом посте я привёл такую возможную форму уличной сетки (взамен надоевшей прямоугольной гипподамовой).

Основная идея - замена прямоугольника как основы всего на пятиугольник. В результате получается более интересная форма регулярности. Не тупая, которая разгадывается с первого раза, а более сложная. А значит, и более красивая. Ибо простота в данном случае хуже воровства.
Основное возражение от читателей - якобы удлинение пути по сравнению с привычным "гипподамом".
Для меня оказалось сложно ответить на это возражение, ибо математику я фундаментально забыл. Не могу привести точную формулу, описывающую средний путь в разных видах геометрического паркета. Напомню, что паркет это замощение плоскости многоугольниками без пробелов и перекрытий. Это можно сделать правильными треугольниками, четырехугольниками (привычная гипподамова сетка улиц) и шестиугольниками. С пятиугольниками сложнее. Правильным пятиугольником плоскость без разрывов не покрыть. Но есть 15 вариантов покрытия плоскости неправильными пятиугольниками.

Вопрос в том, какой из "паркетов" даёт самый короткий путь из случайно выбранных точек А и Б. Мои уважаемые читатели почему то уверены, что оптимален четырехугольный привычный вариант. А я вот совершенно в этом не уверен.

Что влияет на длину пути? Первое, что приходит в голову, количество лучей на перекрёстках. В привычной прямоугольной схеме, где дороги сходятся под прямым углом, от перекрёстка отходят 4 дороги по 4-м направлениям. В треугольной планировке - целых 6.

Это значит, что у нас есть возможность выбрать более точное направление к нашей точки Б. У нас больше вариантов. Выходит, что Треугольник лучше 4-хугольника и намного лучше шестиугольника, где от перекрёстка отходит всего 3 направления.

Но это всё до тех пор, пока мы не установили, что все кварталы равны по площади. И в это момент всё совсем запутывается. Ведь в 6-угольном варианте будет в 2 раза больше перекрёстков, чем в треугольном. Качество компенсируется количеством. И по идее, путь должен быть равным для всех трёх вариантов.
А что у нас с любимыми пятиугольниками? Они, как и следовало ожидать, ровно по середине между четырёх и шестиугольниками. Каждая из схем даёт разное количество перекрёстков с 6, 4 и 3 лучами. И каждая из этих схем скорее всего идентична по пропускной способности и скорости передвижения с привычной гипподамовой сеткой.
А теперь вспомним вариант, который мне больше всего понравился. По причине, о которой я подробно написал в прошлом посте.

Там из пяти перекрёстков 4 - с тремя лучами. И только один с четырьмя. Можно ли улучшить эту схему, чтобы сделать её еще более проницаемой? Лучше, чем положено математикой для "паркетов"? Очень просто. Проделываем очень несложную процедуру. Смотрите на ярко красную линию.
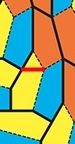
И получаем следующую сетку.

Хуже стало тем, что вместо одного стандартного квартала мы получили 3, отличающихся друг от друга по форме и размеру. Но зато связанность получилась просто потрясающая! Гораздо лучше, чем в привычной схеме. В среднем, из точки А в точку Б можно будет добраться быстрее, чем в привычной схеме с четырёхугольными кварталами.
Я не утверждаю, что моя схема единственно возможная замена "гипподаму". Наверняка их много. Надо только преодолеть зашоренность. Мир многообразен. "Пусть расцветают сто цветов", как говорил председатель Мао.

Основная идея - замена прямоугольника как основы всего на пятиугольник. В результате получается более интересная форма регулярности. Не тупая, которая разгадывается с первого раза, а более сложная. А значит, и более красивая. Ибо простота в данном случае хуже воровства.
Основное возражение от читателей - якобы удлинение пути по сравнению с привычным "гипподамом".
Для меня оказалось сложно ответить на это возражение, ибо математику я фундаментально забыл. Не могу привести точную формулу, описывающую средний путь в разных видах геометрического паркета. Напомню, что паркет это замощение плоскости многоугольниками без пробелов и перекрытий. Это можно сделать правильными треугольниками, четырехугольниками (привычная гипподамова сетка улиц) и шестиугольниками. С пятиугольниками сложнее. Правильным пятиугольником плоскость без разрывов не покрыть. Но есть 15 вариантов покрытия плоскости неправильными пятиугольниками.
Вопрос в том, какой из "паркетов" даёт самый короткий путь из случайно выбранных точек А и Б. Мои уважаемые читатели почему то уверены, что оптимален четырехугольный привычный вариант. А я вот совершенно в этом не уверен.
Что влияет на длину пути? Первое, что приходит в голову, количество лучей на перекрёстках. В привычной прямоугольной схеме, где дороги сходятся под прямым углом, от перекрёстка отходят 4 дороги по 4-м направлениям. В треугольной планировке - целых 6.
Это значит, что у нас есть возможность выбрать более точное направление к нашей точки Б. У нас больше вариантов. Выходит, что Треугольник лучше 4-хугольника и намного лучше шестиугольника, где от перекрёстка отходит всего 3 направления.
Но это всё до тех пор, пока мы не установили, что все кварталы равны по площади. И в это момент всё совсем запутывается. Ведь в 6-угольном варианте будет в 2 раза больше перекрёстков, чем в треугольном. Качество компенсируется количеством. И по идее, путь должен быть равным для всех трёх вариантов.
А что у нас с любимыми пятиугольниками? Они, как и следовало ожидать, ровно по середине между четырёх и шестиугольниками. Каждая из схем даёт разное количество перекрёстков с 6, 4 и 3 лучами. И каждая из этих схем скорее всего идентична по пропускной способности и скорости передвижения с привычной гипподамовой сеткой.
А теперь вспомним вариант, который мне больше всего понравился. По причине, о которой я подробно написал в прошлом посте.

Там из пяти перекрёстков 4 - с тремя лучами. И только один с четырьмя. Можно ли улучшить эту схему, чтобы сделать её еще более проницаемой? Лучше, чем положено математикой для "паркетов"? Очень просто. Проделываем очень несложную процедуру. Смотрите на ярко красную линию.

И получаем следующую сетку.

Хуже стало тем, что вместо одного стандартного квартала мы получили 3, отличающихся друг от друга по форме и размеру. Но зато связанность получилась просто потрясающая! Гораздо лучше, чем в привычной схеме. В среднем, из точки А в точку Б можно будет добраться быстрее, чем в привычной схеме с четырёхугольными кварталами.
Я не утверждаю, что моя схема единственно возможная замена "гипподаму". Наверняка их много. Надо только преодолеть зашоренность. Мир многообразен. "Пусть расцветают сто цветов", как говорил председатель Мао.