SPHO 2007
So SPhO is finally over! :D :D Now just to wait for the results and the practical round right.
For the bored people who love physics, I've typed out the questions. No scanner ><
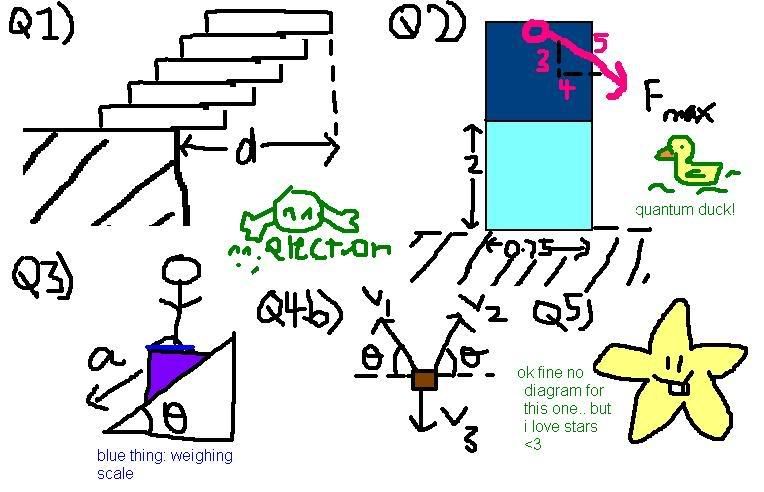
1. You have five (5) blocks of dimension 1 meter by 1 meter and 25 mm thick. What is the furthest you can stack them from the edge of a table before they topple? [8 marks]
2. A column is formed of two marble blocks each weighing 15 kN sitting atop each other as illustrated in the figure 2. A rope to which a force F is applied is attached at the top. The friction coefficient between the marble and the group is u M-G = 0.15 while the friction coefficient between marble and marble is u M-M = 0.20. What is the maximum load Fmax that can be applied? [8 marks]
3. A weighing scale is fixed firmly to a wedge. A person of mass M is standing on the scale. The wedge is on a frictionless inclined ramp that makes an angle to the horizontal as shown in the figure. The system is sliding down the ramp with an acceleration a. The reading of the scale registers the apparent weight of the person. Derive an expression for the apparent weight W of the person as he slides down.
4(a) A projectile is fired from ground level with an initial velocity of Vo at an angle of theta above the horizontal. Show that the maximum height H is given by H = Vo2 sin2 theta / 2g where g is the acceleration of free fall. [4 marks]
4(b) A rocket is projected upwards and explodes into three equally massive fragments just as it reaches the top of its flight. One of the fragments if observed to fall downwards in time t1 as shown in Figure 4 while the other two land after a time t2 after the burst. Determine the height h(t1, t2) at which the fragmentation occurs. [8 marks]
5(a) A feather and a piece of metal of roughly the same size and shape fall with equal acceleration on the Moon but not the Earth. [3 marks]
5(b) Forces between the molecules of a gas cause deviations from ideal gas behavior but forces between the walls of the container do not. [3 marks]
5(c) The sun appears elliptical as it is about to set over a distant horizon. [3 marks]
5 (d) An electric motor in which the armature and field windings are in series slows down more when the load is increased than a motor in which they are in parallel. [3 marks]
6. A circular coil has inner radius R1 and an outer radius R2. The length of the coil is L.
(i) Show that the magnetic induction B at the center when the coil carries a current I is
B = unIL/2 [ln (a + sqrt (a2+b2)) - ln (1 + sqrt (1+b2))]
where a = R2/R1, b = L/2R1 and n is the number of turns per square meter. [10 marks]
(ii) Show that the length of the wire is
l = Vn = 2pi n (a2 -1)bR1^3
7. A ship in a calm port nearing a shore radio station received a 200 MHz signal from the station's antenna. Both station's antenna and the ship's receiving antenna are located 20 m above the sea surface. A succession of maxima and minima are heard in the signal received at the ship. How far is the ship from the station the first time te signal passes through a minimum? How fast is the ship moving if the time between the first minimum and te next one is 50 s? [10 marks]
8. To account for the finite size of molecules and the attractive forces between molecules, Van der Waal devised an equation to describe the gas law for "real" gases
(P + a/V2)(V-b) = RT
where P, V and T are the pressure, volume and temperature of the gas; and R is the universal gas constant.
(a) What are the dimensions of the constants a and b? [4 marks]
(b) Show that the critical point temperature and pressure are given by
Tc = 8a/27bR; Pc = a/27b2 [7 marks]
9(a) Consider an oscillating element of air of cross sectional area A and thickness delta x whose centre is displaced from its equilibrium position by a distance x. We can write the pressure variation of the displaced element as delta p= -B delta V / V where V = A delta x and B is the bulk modulus. The volume change as a result unequal displacements fo the two faces of the element differing by an amount delta s. By applying Newton's law of motion to the element, show that
pv2 = B
where v is the speed of the element and p is the density of the element. [4 marks]
(b) A period of pulsating star may be modeled as a star whose radius R varies periodically with time, performing radial longitudinal pulsations in the fundamental standing wave mode. By analogy with a pipe with one open end, determine the period of the pulsation T in terms of the radius and the average speed of sound in the star matter. For white dwarf stars composed of a material with a bulk modulus of 1.33 x 10^22 Pa and a density of 10^10 kg/m3 and a radius of 9.0 x 10^-3 solar radius, what is the approximate pulsation period of this star? [6 marks]
10. A photon of energy E is scattered from a free stationary electron of rest mass Mo. Show that the maximum kinetic energy of the recoiling electron is given by:
Kmax = E2 / (E + moc2) [8 marks]