Хадлей Викхам. Упорядоченные данные. 4 из 6
Четвертая часть перевода статьи Хадлея Викхама.
4.3. МоделированиеМоделирование является вдохновляющей идеей данной работы, потому что большинство инструментов для моделирования лучше всего работают с упорядоченными массивами данных. Каждый статистический язык содержит способ описания модели как соединения различных переменных - предметно-ориентированный язык, который связывает реакции (responses) с предсказывающими переменными (predictors):
Таблица 14. Два массива данных для выполнения одного и того же теста
id
x
y
1
22,19
24,05
2
19,82
22,91
3
19,81
21,19
4
17,49
18,59
5
19,44
19,85
(а) Данные для двустороннего критерия Стьюдента
Id
Переменная
Значение
1
x
22,19
2
x
19,82
3
x
19,81
4
x
17,49
5
x
19,44
1
y
24,05
2
y
22,91
3
y
21,19
4
y
18,59
5
y
19,85
(б) Данные для модели смешанных эффектов* R (lm()): y ~ a + b + c * d.
* SAS (PROC GLM): y = a + b + c + d + c * d.
* SPSS (glm): y BY a b c d / DESIGN a b c d c * d.
* Stata (regress): y a b c#d.
Это не значит, что для расчета регрессии скрыто используется формат упорядоченных данных. Значительные преобразования производятся для производства числовой матрицы, которая может быть использована для стандартных процедур линейной алгебры. Обычные преобразования включают в себя добавление столбца свободных членов (столбца единиц), обращающих качественные переменные в множество бинарных (индикаторных) переменных, и представление данных в подходящий базис сплайн-функции.
Было несколько попыток адаптировать функции моделирования к специфическим разновидностям неупорядоченных массивов данных. К примеру, в «glm», являющейся процедурой «SAS», множество переменных на стороне реакции (response) в уравнении будет интерпретировано как повторные измерения, если присутствует ключевое слово «REPEATED» (повторено). Для сырых данных Биллборда, мы можем сконструировать модель вида «wk1» - «wk76» = «Композиция» вместо «Ранг» = «Неделя» * «Композиция» на упорядоченных данных.
Другим интересным примером является классический двусторонний критерий Стьюдента, который может быть вычислен двумя способами, в зависимости от того, как хранятся данные. Если данные хранятся как в таблице 14 (а), тогда двусторонний критерий Стьюдента является всего лишь критерием Стьюдента, примененным к средней разнице между x и y. Если они хранятся в виде, аналогичном таблице 14 (б), то эквивалентный результат может быть получен путем наполнения модели смешанных эффектов фиксированными бинарными переменными, представляющими переменную, и случайным пересечением для каждого «id». (В нотации «lmer4» в языке R это выражается как «значение» ~ «переменная» + (1 | «id»)). Оба пути моделирования данных производят тот же результат. Без дополнительной информации мы не можем сказать, которая форма данных является упорядоченной: если x и y представляют длины левой и правой рук, то таблица 14 (а) упорядоченная, если x и y представляют замеры в день 1 и день 10, тогда таблица 14 (б) является упорядоченной.
В то время как вход модели обычно требует упорядоченных входных данных, подобное тщательное внимание обычно не уделяется данным, которые модель выпускает. Выходы, такие как предсказания и оценки коэффициентов, не всегда упорядочены. Это делает более сложным совместное использование результатов разных моделей. К примеру, в языке R, по умолчанию представление коэффициентов модели не упорядочена, потому что не имеет явно названной переменной, которая записывает имя переменной для каждой оценки. Вместо этого они записываются как имена столбцов. В языке R имена столбцов должны быть уникальными, поэтому совместное использование коэффициентов из разных моделей (например, повторный сбор данных в статистическом бутстрэпе или подгруппы) требует обходных маневров, чтобы избежать потери важной информации. Это выбивает вас из течения анализа и делает более трудным совместное использование результатов из множества моделей. В настоящий момент мне неизвестны какие-либо пакеты, решающие эту проблему.
5. Учебный примерСледующий учебный пример показывает, как упорядоченные данные и упорядоченные инструменты делают анализ данных легче за счет облегчения перехода между манипуляцией, визуализацией и моделированием. Тут нет какого-то кода, существующего специально для того, чтобы переделать выход из одной функции в нужный формат для входа в другую. Я покажу вам код языка R, который осуществляет анализ, но даже если вы не очень знакомы с языком R или с конкретными командами, которые я использую, я постараюсь сделать текст легким для понимания за счет тесного переплетения программного кода, результатов и объяснения.
Учебный пример использует данные об индивидуальной смертности в Мексике. Цель состоит в том, чтобы найти причины смерти с необычным паттерном (характером изменения) во времени в течение дня. Рисунок 1 показывает паттерн количества смертей за час, для всех причин смерти. Моя цель состоит в том, чтобы найти болезни, которые наиболее отличаются от этого паттерна.
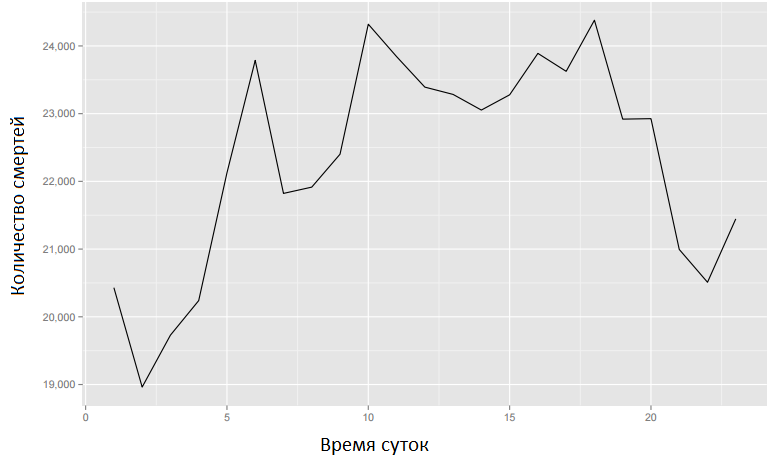
Рисунок 1. Временные паттерны для всех причин смерти.Полный массив данных содержит информацию о 539530 смертях в Мексике в 2008 году и 55 переменных, включая место и время смерти, причину смерти и демографические данные по умершим. Таблица 15 показывает небольшую выборку из этого массива данных, акцентируя внимание на переменных, относящихся ко времени смерти (год, месяц, день, час) и причину смерти - «cod» (cause of death - причина смерти, прим. перев.).
Для достижения нашей цели нахождения необычных временных паттернов мы делаем следующее. Сначала мы считаем количество смертей в каждый час - «hod» (hour of death - час смерти, прим. перев.), и для каждой причины - «cod» - с помощью упорядоченной функции «count».
R> hod2 <- count(deaths, c(“hod”, “cos”))
Таблица 15. Выборка в 16 строк и 5 столбцов из исходного массива данных в 539 530 строк и 55 столбцов
«yod» (year of death - год смерти, прим. перев.)
«mod» (month of death - месяц смерти, прим. перев.)
«dod» (date of death - дата смерти, прим. перев.)
«hod» (hour of death - час смерти, прим. перев.)
«cod» (cause of death - причина смерти, прим. перев.)
2008
1
1
1
B20
2008
1
2
4
I67
2008
1
3
8
I50
2008
1
4
12
I50
2008
1
5
16
K70
2008
1
6
18
I21
2008
1
7
20
I21
2008
1
8
-
K74
2008
1
10
5
K74
2008
1
11
9
I21
2008
1
12
15
I25
2008
1
13
20
R54
2008
1
15
2
I61
2008
1
16
7
I21
2008
1
17
13
I21
После этого мы удаляем из подмассива отсутствующие значения (которые по этой причине для нашей цели неинформативны).
R> hod2 <- subset(hod2, !is.na(hod))
Это приводит к таблице 16(а). Для обеспечения информационных пометок к болезням мы затем объединяем полученный массив данных с массивом «codes», соединенным с переменной «cod». Это добавляет новую переменную, «disease» (болезнь), присутствующую в таблице 16(б).
R> hod2 <- join(hod2, codes, by = "cod")
Общее количество смертей для каждой причины отличается на несколько порядков: случилось 46 794 смерти от сердечного приступа, но только 10 от лавины. Это означает, что имеет смысл сравнивать не общее количество, а скорее пропорцию смертей в каждый час. Мы вычисляем это за счет разбиения массива данных по переменной «cod» и затем используем глагол «transform()» (преобразовать), добавляя новый столбец «prop», частоту в час, деленную на общее количество смертей от этой причины. Этот новый столбец - таблица 16(в).
Функция «ddply()» разбивает первый аргумент («hod2») по второму аргументу (переменной «cod») и затем применяет третий аргумент («transform») к каждому получившемуся фрагменту. Четвертый аргумент (prop = freq / dum(freq)) затем применяется к результатам работы «transform()».
R> hod2 <- ddply(hod2, "cod", transform, prop = freq / sum(freq))
Затем мы вычисляем средний общий уровень смертности для каждого часа и вливаем его назад в исходный массив данных. Это дает нам таблицу 16 (г). Сравнением «prop» с «prop_all» мы можем легко сравнить каждую болезнь с паттерном для общей смертности.
Сначала, мы вычисляем количество людей, умирающих каждый час. Мы разбиваем «hod2» по «hod» и вычисляем сумму по каждой причине смерти.
R> overall <- ddply(hod2, "hod", summarise, freq_all = sum(freq))
Затем, мы вычисляем общую пропорцию людей, умирающих каждый час:
R> overall <- transform(overall, prop_all = freq_all / sum(freq_all))
Наконец, мы соединяем общий массив данных с индивидуальным массивом для того, чтобы было их легче сравнить:
R> hod2 <- join(hod2, overall, by = "hod")
Таблица 16. Выборка из четырех болезней и четырех часов из массива данных «hod2»
hod
cod
freq
8
B16
4
8
E84
3
8
I21
2205
8
N18
315
9
B16
7
9
E84
1
9
I21
2209
9
N18
333
10
B16
10
10
E84
7
10
I21
2434
10
N18
343
11
B16
6
11
E84
3
11
I21
2128
(a)
болезнь
prop
freq_all
prop_all
Острый гепатит B
0,04
21915
0,04
Кистозный фиброз
0,03
21915
0,04
Острый инфаркт миокарда
0,05
21915
0,04
Хроническая почечная недостаточность
0,04
21915
0,04
Острый гепатит B
0,07
22401
0,04
Кистозный фиброз
0,01
22401
0,04
Острый инфаркт миокарда
0,05
22401
0,04
Хроническая почечная недостаточность
0,04
22401
0,04
Острый гепатит B
0,10
24321
0,05
Кистозный фиброз
0,07
24321
0,05
Острый инфаркт миокарда
0,05
24321
0,05
Хроническая почечная недостаточность
0,04
24321
0,05
Острый гепатит B
0,06
23843
0,05
Кистозный фиброз
0,03
23843
0,05
Острый инфаркт миокарда
0,05
23843
0,05
(б), (в), (г)
Далее мы вычисляем расстояние между временными паттернами каждой причины смерти и общим временным паттерном. Существует множество способов измерить это расстояние, но я обнаружил, что с этим хорошо справляется простое среднеквадратичное отклонение. Мы также записали размер выборки, т.е. общее количество от этой причины. Чтобы гарантировать, что болезни, которые мы рассматриваем, достаточно репрезентативны, мы работаем только с болезнями с общим количеством смертей более 50 (т.е. примерно по 2 в час).
R> devi <- ddply(hod2, "cod", summarise,
R> n = sum(freq),
R> dist = mean((prop - prop_all)^2))
R>
R> devi <- subset(devi, n > 50)
Мы не знаем характеристики дисперсии этой оценочной функции, но мы можем исследовать ее визуально, нанеся на график «n» и «dist» (дистанцию), рисунок 2 (а). На линейной шкале график показывает довольно мало, кроме того, что изменчивость меняется с увеличением размера выборки. Но на двойной логарифмической шкале, рисунок 2 (б), паттерн довольно ясен. Увидеть паттерн особенно легко, когда мы добавляем линию наибольшего соответствия из грубой линейной модели.
Продолжение следует
4.3. МоделированиеМоделирование является вдохновляющей идеей данной работы, потому что большинство инструментов для моделирования лучше всего работают с упорядоченными массивами данных. Каждый статистический язык содержит способ описания модели как соединения различных переменных - предметно-ориентированный язык, который связывает реакции (responses) с предсказывающими переменными (predictors):
Таблица 14. Два массива данных для выполнения одного и того же теста
id
x
y
1
22,19
24,05
2
19,82
22,91
3
19,81
21,19
4
17,49
18,59
5
19,44
19,85
(а) Данные для двустороннего критерия Стьюдента
Id
Переменная
Значение
1
x
22,19
2
x
19,82
3
x
19,81
4
x
17,49
5
x
19,44
1
y
24,05
2
y
22,91
3
y
21,19
4
y
18,59
5
y
19,85
(б) Данные для модели смешанных эффектов* R (lm()): y ~ a + b + c * d.
* SAS (PROC GLM): y = a + b + c + d + c * d.
* SPSS (glm): y BY a b c d / DESIGN a b c d c * d.
* Stata (regress): y a b c#d.
Это не значит, что для расчета регрессии скрыто используется формат упорядоченных данных. Значительные преобразования производятся для производства числовой матрицы, которая может быть использована для стандартных процедур линейной алгебры. Обычные преобразования включают в себя добавление столбца свободных членов (столбца единиц), обращающих качественные переменные в множество бинарных (индикаторных) переменных, и представление данных в подходящий базис сплайн-функции.
Было несколько попыток адаптировать функции моделирования к специфическим разновидностям неупорядоченных массивов данных. К примеру, в «glm», являющейся процедурой «SAS», множество переменных на стороне реакции (response) в уравнении будет интерпретировано как повторные измерения, если присутствует ключевое слово «REPEATED» (повторено). Для сырых данных Биллборда, мы можем сконструировать модель вида «wk1» - «wk76» = «Композиция» вместо «Ранг» = «Неделя» * «Композиция» на упорядоченных данных.
Другим интересным примером является классический двусторонний критерий Стьюдента, который может быть вычислен двумя способами, в зависимости от того, как хранятся данные. Если данные хранятся как в таблице 14 (а), тогда двусторонний критерий Стьюдента является всего лишь критерием Стьюдента, примененным к средней разнице между x и y. Если они хранятся в виде, аналогичном таблице 14 (б), то эквивалентный результат может быть получен путем наполнения модели смешанных эффектов фиксированными бинарными переменными, представляющими переменную, и случайным пересечением для каждого «id». (В нотации «lmer4» в языке R это выражается как «значение» ~ «переменная» + (1 | «id»)). Оба пути моделирования данных производят тот же результат. Без дополнительной информации мы не можем сказать, которая форма данных является упорядоченной: если x и y представляют длины левой и правой рук, то таблица 14 (а) упорядоченная, если x и y представляют замеры в день 1 и день 10, тогда таблица 14 (б) является упорядоченной.
В то время как вход модели обычно требует упорядоченных входных данных, подобное тщательное внимание обычно не уделяется данным, которые модель выпускает. Выходы, такие как предсказания и оценки коэффициентов, не всегда упорядочены. Это делает более сложным совместное использование результатов разных моделей. К примеру, в языке R, по умолчанию представление коэффициентов модели не упорядочена, потому что не имеет явно названной переменной, которая записывает имя переменной для каждой оценки. Вместо этого они записываются как имена столбцов. В языке R имена столбцов должны быть уникальными, поэтому совместное использование коэффициентов из разных моделей (например, повторный сбор данных в статистическом бутстрэпе или подгруппы) требует обходных маневров, чтобы избежать потери важной информации. Это выбивает вас из течения анализа и делает более трудным совместное использование результатов из множества моделей. В настоящий момент мне неизвестны какие-либо пакеты, решающие эту проблему.
5. Учебный примерСледующий учебный пример показывает, как упорядоченные данные и упорядоченные инструменты делают анализ данных легче за счет облегчения перехода между манипуляцией, визуализацией и моделированием. Тут нет какого-то кода, существующего специально для того, чтобы переделать выход из одной функции в нужный формат для входа в другую. Я покажу вам код языка R, который осуществляет анализ, но даже если вы не очень знакомы с языком R или с конкретными командами, которые я использую, я постараюсь сделать текст легким для понимания за счет тесного переплетения программного кода, результатов и объяснения.
Учебный пример использует данные об индивидуальной смертности в Мексике. Цель состоит в том, чтобы найти причины смерти с необычным паттерном (характером изменения) во времени в течение дня. Рисунок 1 показывает паттерн количества смертей за час, для всех причин смерти. Моя цель состоит в том, чтобы найти болезни, которые наиболее отличаются от этого паттерна.

Рисунок 1. Временные паттерны для всех причин смерти.Полный массив данных содержит информацию о 539530 смертях в Мексике в 2008 году и 55 переменных, включая место и время смерти, причину смерти и демографические данные по умершим. Таблица 15 показывает небольшую выборку из этого массива данных, акцентируя внимание на переменных, относящихся ко времени смерти (год, месяц, день, час) и причину смерти - «cod» (cause of death - причина смерти, прим. перев.).
Для достижения нашей цели нахождения необычных временных паттернов мы делаем следующее. Сначала мы считаем количество смертей в каждый час - «hod» (hour of death - час смерти, прим. перев.), и для каждой причины - «cod» - с помощью упорядоченной функции «count».
R> hod2 <- count(deaths, c(“hod”, “cos”))
Таблица 15. Выборка в 16 строк и 5 столбцов из исходного массива данных в 539 530 строк и 55 столбцов
«yod» (year of death - год смерти, прим. перев.)
«mod» (month of death - месяц смерти, прим. перев.)
«dod» (date of death - дата смерти, прим. перев.)
«hod» (hour of death - час смерти, прим. перев.)
«cod» (cause of death - причина смерти, прим. перев.)
2008
1
1
1
B20
2008
1
2
4
I67
2008
1
3
8
I50
2008
1
4
12
I50
2008
1
5
16
K70
2008
1
6
18
I21
2008
1
7
20
I21
2008
1
8
-
K74
2008
1
10
5
K74
2008
1
11
9
I21
2008
1
12
15
I25
2008
1
13
20
R54
2008
1
15
2
I61
2008
1
16
7
I21
2008
1
17
13
I21
После этого мы удаляем из подмассива отсутствующие значения (которые по этой причине для нашей цели неинформативны).
R> hod2 <- subset(hod2, !is.na(hod))
Это приводит к таблице 16(а). Для обеспечения информационных пометок к болезням мы затем объединяем полученный массив данных с массивом «codes», соединенным с переменной «cod». Это добавляет новую переменную, «disease» (болезнь), присутствующую в таблице 16(б).
R> hod2 <- join(hod2, codes, by = "cod")
Общее количество смертей для каждой причины отличается на несколько порядков: случилось 46 794 смерти от сердечного приступа, но только 10 от лавины. Это означает, что имеет смысл сравнивать не общее количество, а скорее пропорцию смертей в каждый час. Мы вычисляем это за счет разбиения массива данных по переменной «cod» и затем используем глагол «transform()» (преобразовать), добавляя новый столбец «prop», частоту в час, деленную на общее количество смертей от этой причины. Этот новый столбец - таблица 16(в).
Функция «ddply()» разбивает первый аргумент («hod2») по второму аргументу (переменной «cod») и затем применяет третий аргумент («transform») к каждому получившемуся фрагменту. Четвертый аргумент (prop = freq / dum(freq)) затем применяется к результатам работы «transform()».
R> hod2 <- ddply(hod2, "cod", transform, prop = freq / sum(freq))
Затем мы вычисляем средний общий уровень смертности для каждого часа и вливаем его назад в исходный массив данных. Это дает нам таблицу 16 (г). Сравнением «prop» с «prop_all» мы можем легко сравнить каждую болезнь с паттерном для общей смертности.
Сначала, мы вычисляем количество людей, умирающих каждый час. Мы разбиваем «hod2» по «hod» и вычисляем сумму по каждой причине смерти.
R> overall <- ddply(hod2, "hod", summarise, freq_all = sum(freq))
Затем, мы вычисляем общую пропорцию людей, умирающих каждый час:
R> overall <- transform(overall, prop_all = freq_all / sum(freq_all))
Наконец, мы соединяем общий массив данных с индивидуальным массивом для того, чтобы было их легче сравнить:
R> hod2 <- join(hod2, overall, by = "hod")
Таблица 16. Выборка из четырех болезней и четырех часов из массива данных «hod2»
hod
cod
freq
8
B16
4
8
E84
3
8
I21
2205
8
N18
315
9
B16
7
9
E84
1
9
I21
2209
9
N18
333
10
B16
10
10
E84
7
10
I21
2434
10
N18
343
11
B16
6
11
E84
3
11
I21
2128
(a)
болезнь
prop
freq_all
prop_all
Острый гепатит B
0,04
21915
0,04
Кистозный фиброз
0,03
21915
0,04
Острый инфаркт миокарда
0,05
21915
0,04
Хроническая почечная недостаточность
0,04
21915
0,04
Острый гепатит B
0,07
22401
0,04
Кистозный фиброз
0,01
22401
0,04
Острый инфаркт миокарда
0,05
22401
0,04
Хроническая почечная недостаточность
0,04
22401
0,04
Острый гепатит B
0,10
24321
0,05
Кистозный фиброз
0,07
24321
0,05
Острый инфаркт миокарда
0,05
24321
0,05
Хроническая почечная недостаточность
0,04
24321
0,05
Острый гепатит B
0,06
23843
0,05
Кистозный фиброз
0,03
23843
0,05
Острый инфаркт миокарда
0,05
23843
0,05
(б), (в), (г)
Далее мы вычисляем расстояние между временными паттернами каждой причины смерти и общим временным паттерном. Существует множество способов измерить это расстояние, но я обнаружил, что с этим хорошо справляется простое среднеквадратичное отклонение. Мы также записали размер выборки, т.е. общее количество от этой причины. Чтобы гарантировать, что болезни, которые мы рассматриваем, достаточно репрезентативны, мы работаем только с болезнями с общим количеством смертей более 50 (т.е. примерно по 2 в час).
R> devi <- ddply(hod2, "cod", summarise,
R> n = sum(freq),
R> dist = mean((prop - prop_all)^2))
R>
R> devi <- subset(devi, n > 50)
Мы не знаем характеристики дисперсии этой оценочной функции, но мы можем исследовать ее визуально, нанеся на график «n» и «dist» (дистанцию), рисунок 2 (а). На линейной шкале график показывает довольно мало, кроме того, что изменчивость меняется с увеличением размера выборки. Но на двойной логарифмической шкале, рисунок 2 (б), паттерн довольно ясен. Увидеть паттерн особенно легко, когда мы добавляем линию наибольшего соответствия из грубой линейной модели.
Продолжение следует