Сквозит двойная бесконечность из отраженной глубины
Георг Кантор был первым, кто осознал, что бесконечности тоже бывают разного «размера». Самая «маленькая», фундаментальная бесконечность - множество натуральных чисел. А вот множество всех подмножеств этого множества представляет собой уже следующую ступень: его элементы нельзя пересчитать - поставить в однозначное соответствие числам натурального ряда. Переходя к множеству подмножеств снова и снова, мы поднимаемся по бесконечной лестнице бесконечностей.
Кантор верил, что действительные числа - от Бога, и, похоже, именно эта вера и свела его сначала с ума, а потом в могилу. Он доказал, что совокупность действительных чисел - континуум - превышает по своей мощности множество натуральных. Но где именно она располагается в иерархии бесконечностей, какую ступень занимает?
Кантор попеременно то почти доказывал, то почти исключал, что вторую - но так и не смог придти к окончательному выводу. Неудивительно: через полвека после его смерти Пол Коэн установит неразрешимость этой задачи в системе принятых аксиом - и получит Филдсовскую премию. А Кантор, с его верой в божественное происхождение чисел, наверное, просто не мог допустить подобной несуразности.
Автор книжки, излагающей эту историю, тоже пытается отстаивать объективное существование чисел. Аргументирует он от противного: если бы числа были просто нашим изобретением, то все их свойства были бы нам уже заранее известны; на деле же мы постоянно открываем что-то новое. Похоже, он совсем забыл ожившего монстра доктора Франкенштейна :)
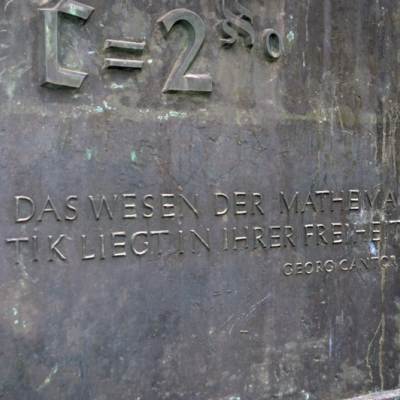
Девиз Кантора, высеченный на памятнике ему в Халле: «Свобода - вот сущность математики» (фото с сайта Halle im Bild). А формула - математическая запись утверждения, что континуум располагается на второй ступеньке лестницы бесконечностей.
Спасибо уважаемому evgeniirudnyi за наводку на книжку.