Ещё раз о рентгенологической оценке сколиотической деформации позвоночника - I
Продолжение: http://healthy-back.livejournal.com/156119.html
http://www.spinalsystems.ru/library/forspecialists/forspecialists_41.html М.В. Михайловский, С.А. Шуц
«ОртоЛайн», ООО, Орто-техническая лаборатория позвоночника.
Представлен анализ источников грубых ошибок оценки дуги по методике Cobb, могущих приводить к 100% и большей погрешности при измерении величины деформации. Показаны причины невозможности корректной оценки деформации позвоночника по угловому параметру. Даны негативные примеры последствий таких измерений.
Предложен альтернативный метод - метод оценки по параметру кривизны дуги (К.Д. метод). Доказана инвариантность метода, высокая точность оценки и доступность для применения в широкой врачебной практике. Предложено несколько вариантов технического обеспечения для проведения измерений, отличающихся степенью автоматизации и объемами получаемой информации. Предложен подробный классификатор оценки степени деформации по результатам спондилометрии.
Here, we present the analysis of sources of serious errors in the Cobb method of arch evaluation, which can lead to errors of 100% or higher in deformation measurements. The reasons of the impossibility to correctly evaluate spinal curvature under the angular parameter are shown. We also propose an alternative method - the method of evaluation by the arch curvature parameter (AC method). The method's invariance is proven as well as its high evaluation accuracy and the availability for usage in general medical practice. We also propose several types of hardware for the measurements, distinguished by the levels of automation and data provision capabilities. A detailed classifier for defining a degree of deformation in accordance with the spondylometry results is proposed.
Деформация (искривленность) позвоночника является решающим фактором при оценке степени заболевания, назначении вида лечения, назначения пособия по инвалидности, оценки результатов лечения и т.д. Следовательно, все понятия, связанные с деформацией, методы и технические средства определения деформации, терминологические условности и допущения должны быть однозначно определены и решены на надежном уровне. Если внимательно просмотреть различные медицинские документы, упоминающие деформацию позвоночника, можно заметить, как мы еще далеки от указанных требований. Более того, в описаниях спондилограмм даже не предусмотрена норма, обязывающая аналитика указывать тип оценочного параметра и тип классификатора степени заболевания.
Оценочный параметр искривленности позвоночника, как во фронтальной, так и в сагиттальной плоскости, несет ответственность за достоверность функциональную (степень патологичности) и физическую (точность представления). В связи с этим к настоящему времени сформировались многокомпонентные оценки патологической деформации позвоночника. Однако наиболее представительными являются клиническая картина и рентгенологическое обследование.
В этой статье речь идет именно о второй из перечисленных компонент, которая по частоте применения стоит на одном из первых мест. Столь ответственная роль показателя деформации налагает на него обязанность обладания высоким уровнем метрологических свойств таких как:
- представительность - способность показателя оценивать свойство объекта однозначно и максимально полно,
- технологичность, т.е. технологическое удобство его определения,
- точность оценки. В частности, если одна степень сколиоза по показателю угла Cobb перекрывается соседней (например, вторая и третья) величиной в 5˚, то точность измерения угла дуги должна быть хотя бы в половину этого интервала, т.е. 2.5˚ Cobb,
- логичность. Широкий пользователь показателя искривленности позвоночника должен
легко и просто представлять себе смысл результата измерений.
К сожалению, используемые в настоящее время рентгенологические показатели искривленности позвоночника оказались настолько далеки от перечисленных требований, что заставляют еще раз вернуться к тщательному анализу качества оценок деформации, возможным последствиям ошибок и, при необходимости, поиску альтернативных методов.
Итак, предметом обсуждения является траектория цепочки последовательно выстроенных позвонков и промежутков между ними в результате, подчеркиваем, взаимного перемещения сегментов позвоночника в процессе роста туловища. Такую цепочку правильнее было бы ассоциировать с дугой, являющей кривую линию выстроенных позвонков. Для дуги характерна форма, которая может быть описана математической функцией с различной степенью аппроксимации. Однако, дуга может быть лишь частью позвоночника; кроме нее могут быть еще другая дуга и не изогнутые участки позвоночного столба. Для этого случая поиск аппроксимации полной линии позвоночника, во-первых, достаточно сложен, а во-вторых - не представляет практического интереса, так как столь сложная кривая должна быть
математически описана большим количеством параметров. В дальнейшем сравнивать эту кривую с другими (других пациентов), будет чрезвычайно сложно и трудоемко. Гораздо удобнее и достаточно ограничиться лишь описанием каждого криволинейного участка, имеющих, как правило, тангенциальное сопряжение между собой.
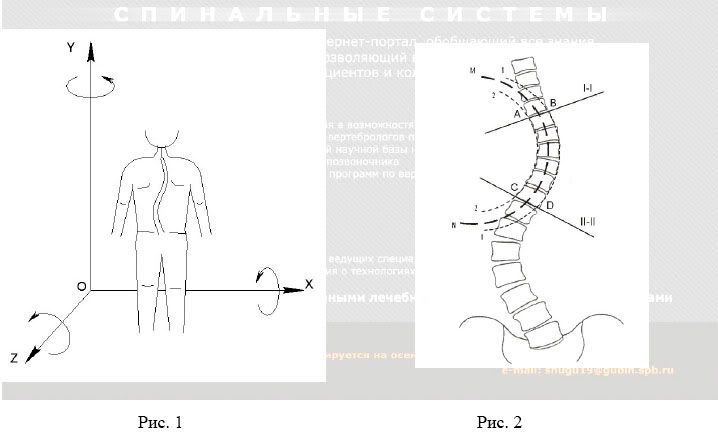
Для однозначного толкования ряда положений и процессов, определим положение туловища в некоторой системе координат, согласно рис. 1. Напомним, что поворот позвонка вокруг оси позвоночника - условно, вокруг вертикальной оси Y, называется ротацией. Поворот позвонка вокруг горизонтальной оси, лежащей в сагиттальной плоскости (YOZ) - условно, вокруг оси Z, принято называть латерофлексией. Ось латерофлексии проходит через центр тела позвонка. Групповой поворот позвонков вокруг горизонтальной оси, лежащей во фронтальной плоскости (YOX) - условно, вокруг оси X, с одновременным перемещением по оси Z (в плоскости YOZ), определяет сагиттальные изгибы - кифоз и лордоз.
Наконец, нужно договориться о том, какую кривую мы должны принять для описания траектории позвонков в дуге (рис. 2) - внешнюю латеральную I-I, аппроксимирующую выпуклую поверхность дуги, внутреннюю II-II, аппроксимирующую вогнутую поверхность дуги или какую-либо промежуточную? По ряду очевидных причин было бы удобней траекторией позвонков в дуге считать кривую линию M-N, аппроксимирующую центры позвонков на фронтальной проекции позвоночника. Длина сколиотической дуги определяется траекторией дуги M-N, заключенной между сечениями I-I и II-II, определяющими точку сопряжения рассматриваемой дуги с соседней дугой или прямым участком позвоночника.
Для оценки кифотической компоненты деформации договоримся использовать внешнее очертание дуги - по типу кривой I-I на рис.2.
Ниже нам еще придется принять ряд определений, а сейчас рассмотрим основные практические методы оценки деформации позвоночника с точки зрения их функциональной добротности. Речь пойдет в первую очередь о методе Фергюссона (угол Δ на рис. 3а) и методе Кобба (угол α на рис. 3в), как наиболее представительных и массово применяемых рентгенологами и ортопедами. На этих рисунках отражены схемы измерений углов дуги в качестве параметра представляющего деформацию позвоночника в области рассматриваемой дуги.
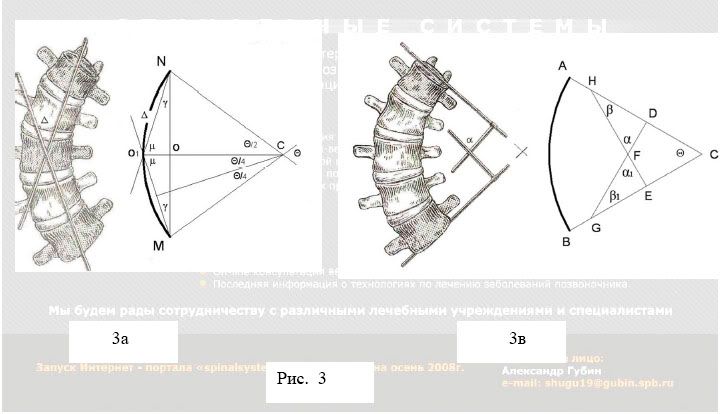
Геометрические построения на рис.3 - модели методов [2], являются теоретическими представлениями, в то время как, методические приемы обследования рентгенограмм могут существенно, как будет показано ниже, искажать модель оценки угла.
Общим для методов является то, что оба они представляют дугу как часть окружности, аппроксимирующей криволинейность позвоночника. Оба метода предполагают в качестве оценочного параметра угловое значение дуги, полученное путем геометрических построений сторон угла охвата дуги на рентгенограмме. Наконец, оба метода предполагают систему ранжирования диапазона измеряемых величин по группам, для присвоения каждой группе некоторой степени патологичности заболевания - в частности, степени сколиоза. Несмотря на то, что принципы ранжирования измеренных углов - классификатор степени деформации, являются заслугой отдельного автора, полезно имя автора классификатора увязывать с именем автора метода измерений деформации для придания однозначности системы оценки. Жаль, что в рутинной работе с различного рода справками, заключениями и прочим, практически никогда не указывается тип (имя) классификатора степени.
Подразумевается, что при угловых оценках дуги используется классификатор В.Д. Чаклина как универсальный инструмент, что уже является грубой ошибкой. Классификация В.Д. Чаклина была сделана применительно к оценкам, полученным использованием метода Кобба [8], а практически используется для оценок, сделанных каждым методом.
Метод Фергюссона, рис. 3а, использует для оценки три точки дуги - две на концах дуги и одну в центре. Угол, заключенный между пересекающимися хордами дуги является оценочным параметром дуги. Достоинством метода является независимая оценка и, соответственно, однозначность представления измеряемой дуги. Следует иметь в виду, что строго математически, построенный угол Фергюссона «Δ», равен точно половине угла «α» (либо Θ), т.е. половине теоретического угла Кобба.. Назовем этот угол геометрическим углом или просто - угол дуги.
Для практических измерений метод Кобба использует для построения краниальные поверхности тел нейтральных позвонков и является зависимой оценкой. Нейтральным - концевым в дуге, принимается характерный позвонок, у которого замыкательные пластинки максимально параллельны. На нейтральных верхнем и нижнем позвонках строятся образующие оценочного угла - аналог АС и ВС на модели (рис. 3в), либо перпендикуляры к образующим угла для получения того же угла охвата дуги. На обывательском уровне можно, указать на простоту построений угла в качестве достоинств метода Кобба и обоснования его популярности. На самом деле, квалифицированные ортопеды хорошо знают, что оценка по Коббу во многом зависит от качественного определения нейтральных позвонков в дуге, от идентичности построения на различных пленках, от качества построений и др. Но, состоятельность этой оценки, даже при скрупулезно правильном построении, вызывает большие сомнения. Мы, в частности, неоднократно сталкивались с противоречием вызванным величиной корректно измеренного угла Кобба и клинической картиной заболевания. Поэтому, поставили задачу тщательного анализа метода Кобба и ниже представляем результаты этого анализа.
Но, прежде вспомним основные понятия и параметры, связанные с дугой [1]. Применительно к нашей задаче обозначим дугу как участок плоской кривой линии, обладающей свойством непрерывности и монотонно изменяющей направление. На рис. 4а показана линия L, на которой выделен участок M-N перемещения (огибания) касательной Р её дуги из точки M в N с поворотом на угол φ.
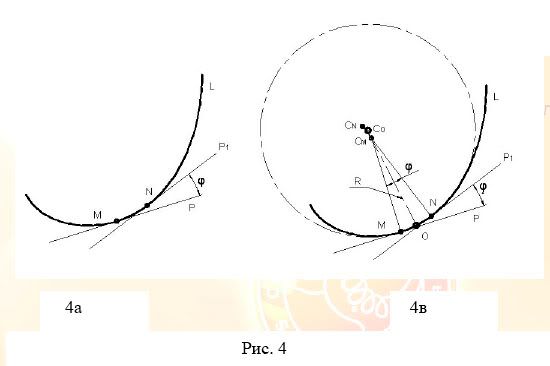
Отношение угла φ к длине дуги M-N показывает степень искривления линии L на участке M-N и представляет собой среднюю кривизну дуги. В общем случае принято говорить о кривизне дуги в любой произвольно выбранной точке, для нахождения которой требуются определенные математические решения. В результате можно получить так называемый радиус кривизны - отрезки М-СМ и N- CN соответственно для точек M и N дуги, на рис. 4в. [3].
Кривизну дуги в произвольной точке можно представить только в дифференциальном виде. Множество таких представлений позволяет описать конкретную дугу, но вот сравнивать ее с любой другой дугой можно только по множеству параметров.
Их отыскания связанно с решением уравнений касательных к точкам кривой, уравнений перпендикуляров к касательным, поиском координат центров кривизны и др. Несомненно, что, в соответствие с моделями методов Кобба и Фергюссона, рассматривать нужно окружность, которой аппроксимирована дуга. Это резко упрощает анализ и дает возможность сравнивать все возможные случаи по одному лишь параметру, причем с достаточной для рутинной практики точностью.
Важно закрепить, что геометрическое положение ряда позвонков определяет траекторию, ассоциированную с дугой, которая имеет свойство кривизны и в каждой точке однозначно выражается через соответствующий радиус кривизны. Для окружности радиус кривизны имеет постоянное в любой точке значение. Образующие геометрического угла являются радиальными линиями окружности, а вершина угла обязательно находится в центре окружности.
Вернемся к разговору об эффективности оценок деформации позвоночника. Рассмотрим последовательно источники ошибок метода Кобба, начиная с самой малозначимой. Ошибкой оценки мы будем считать разницу измеренных значений угла дуги в соответствии с приемами конкретной методики (в частности Кобба) и геометрическим значением угла дуги в соответствие с моделью оценки по рис. 3. Разумеется, речь здесь идет о методической компоненте общей ошибки, которая не связана с техникой разрисовки R-граммы конкретным человеком.
Первая ошибка связана с тем, что на практике образующие угла Кобба не являются радиальными линиями аппроксимирующей окружности. На рис. 5 показана дуга с ярко выраженным граничным позвонком, т.е. позвонком с нулевой клиновидностью или, что одно и то же, с параллельными замыкательными гранями. По условиям метода Кобба образующая угла проводится по одной из параллельных - внешней грани. Но, геометрически не существует двух параллельных радиальных линий, проведенных из разных точек окружности. Если позвонок расположен симметрично относительно дуги, т.е. в плоскости YOX грани позвонка перпендикулярны касательной дуги в точке F (рис. 5), то единственной радиальной линией, совмещенной с направлением позвонка в дуге - нейтралью позвонка, может быть только линия F-O, проходящая через центр тяжести сечения позвонка. Нетрудно видеть, что проведенная через внешнюю крайнюю поверхность граничного позвонка прямая М-О1 отражает угол охвата только части искомой дуги - дуги FG с центром в т. «О». Линия М-О1, проведенная по внешней грани позвонка занижает искомый угол охвата дуги. Угол охвата полной дуги (Г.У.) - дуги M-N, при построениях по Коббу будет занижен в нашем случае с 67˚ до 60˚. Реальная ошибка этого фактора на практике составляет 10-15%, причем всегда в меньшую сторону.
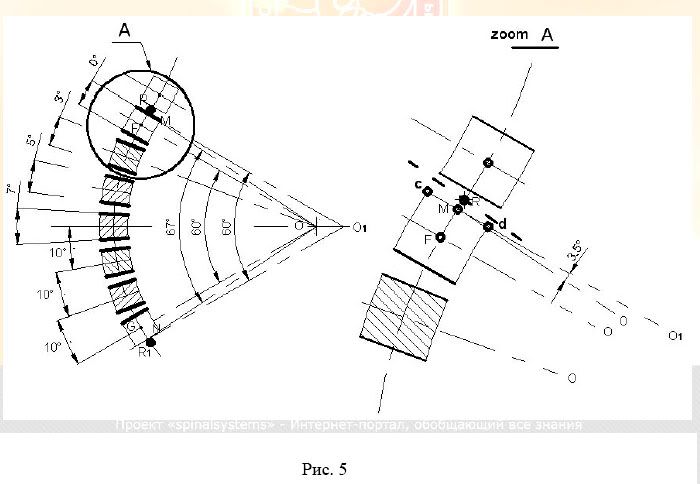
Вторая ошибка метода Кобба, гораздо большей величины, так же связана с тем, что построения указанным способом отражают одновременно вклад двух факторов: криволинейность дуги и особенности локального положения позвонка в дуге, рис. 6. Речь идет о повороте краниального позвонка дуги вокруг оси Z, рис. 1 - влиянии латерофлексии.
Мы провели множество измерений деформации позвоночника методом Кобба и параллельно расчетным методом оценивали величину геометрического угла дуги по рис. 3в. Оказалось, что соотношение угла дуги и угла Кобба находилось в интервале 0.4 - 3,1. Это искажения реального угла дуги, упакованные в обертку с именем «угол Кобба», включающие группу ошибок этого метода.
Второе существо ошибки можно объяснить следующим. Деформация позвоночника происходит под воздействием системы сил различных категорий. Провоцирующая система сил стремиться увеличить кривизну дуги, что мы часто наблюдаем. Параллельно с этой системой сил работает другая - препятствующая (удерживающая) росту деформации. В результате противоборства сил позвонки в дуге несколько поворачиваются вокруг оси Z, причем тем больше, чем местоположение позвонка в дуге ближе к концам дуги (рис.6). Если внимательно посмотреть рентгенограммы позвоночника, то эти угловые повороты легко заметить.

При расчерчивании R-граммы по методу Кобба повороты позвонков, как и в предыдущем случае, приводят к занижению искомого угла. На рис. 6 измеренный угол Кобба составил 46˚, а угол дуги 67˚. Реальная ошибка по описанной причине может составить более 50%, причем, как и в первом случае, всегда в сторону занижения угла дуги.
Третья ошибка метода Кобба вызвана не корректным и грубым графическим обобщением сильно разнородных участков дуги, что также является отступлением от модели метода по рис. 3в.
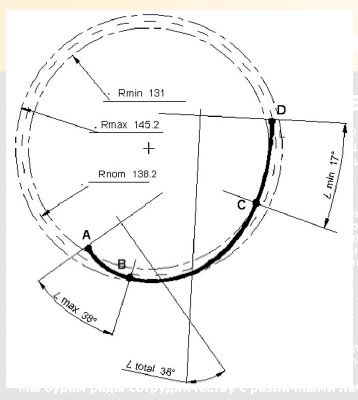
На рис. 7 представлен наиболее частый случай - асимметричная по высоте дуга. На ней условно выделены три участка: один - А-В, большой кривизны, а другой - C-D, малой кривизны. Между этими участками лежит участок усреднения B-C. Условно для каждого участка проведены построения для измерения угла. (Я не увидел или не понял как предлагемый метод учитывает этот нюанс - H.B.)
Как видно на этом рисунке разница угла по Коббу между участками высокой и низкой кривизны составляет более двух раз. Измеренная по Коббу полная дуга А-D показывает максимальную криволинейность участка А-В.
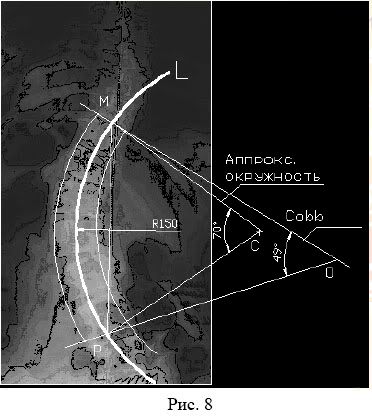
Практический пример проявления 2-ой и 3-ей ошибок представлен на спондилограмме, рис.8. На нем видна разница между моделью и реализацией метода Кобба. Для случаев, подобных изображенному на рис. 7, уместно задать вопрос: «А насколько корректно конечный результат отражает реальную криволинейность дуги, если почти треть её длинны составляет только половину от измеренного и еще треть длинны составляют еще, например, 40% от измеренной величины дуги?».
Очевидно, что измерения по Коббу асимметричной дуги сильно искажают (в примере по рис.7, более двух раз) представления о реальной криволинейности дуги.
Забегая вперед, отметим, что если воспользоваться параметром кривизны дуги, для примера по рис. 7, то результат оценки деформации кардинально меняется. Как видно на рисунке, радиус аппроксимирующей окружности, касающейся внешнего контура дуги, отличается от того же, касающейся внутреннего контура дуги, на величину 145.2-131= 14.2 мм. Отличие от среднего радиуса (138.2 мм) не превышает ±5%. Это максимальная погрешность оценки, которую мы можем получить путем самых грубых построений. Заметим, что на рисунке 7 представлен, может быть, запредельный по асимметрии случай для реальной дуги. Это только подчеркивает, что в практике ортопеда точность оценки дуги по параметру кривизны будет еще выше.
Следующую ошибку метода Кобба, как, впрочем, и метода Фергюссона, следует ассоциировать с принципиальной методической ошибкой. Ниже мы приводим аргументы в знак того, что для оценки дуги, с точки зрения потенциала прогрессирования или устойчивости, нельзя в качестве оценочного параметра использовать угол охвата дуги. Его, этот угол, нужно обязательно соотнести (разделить на) с длиной дуги или напрямую пользоваться для оценки параметром кривизны дуги.
На рис. 9 показано семейство пропорциональных дуг, расположенных в поле одного и того же угла и отличающихся только радиусом аппроксимирующей окружности. В таблице 1, прямо под рисунком, представлены характеристики этих дуг.

Как видно из таблицы, кривизна дуг увеличивается в направлении от №1 к №6, а соотношение высоты и глубины дуги в пределах постоянного угла дуги - постоянно.
Авторов метода Кобба, видимо, спровоцировало, что соотношение H/B любой из дуг в поле конкретного угла - постоянно, и это было принято за факт равной устойчивости к возможному прогрессированию деформации. Обманчивый вывод состоял в том, что принципиальным и достаточным параметром для оценки дуги является ее угол. В этих рассуждениях упущен факт увеличения устойчивости дуги к прогрессированию при уменьшении ее реальной кривизны. Дуга с большим радиусом, имеет меньшую кривизну и, логически, меньшую патологичность. На рис. 9 дуга №4 умышленно продлена до положения c-d для удобства сравнения ее с дугой 1 (c' - d'). Легко видеть разницу кривизны этих дуг. Дуга №6 с наименьшим радиусом, т.е. большей кривизной, является наиболее патологичной и имеет меньшую сопротивляемость к изгибу. (Авторам нельзя отказать в знании геометрии, но я не вижу знания физики. Длинная дуга большого диаметра соответствует большому же смещению центра тяжести, что очень странно рассматривать как небольшую патологичность. Добавьте сюда тот факт, что большая дуга - это признак бОльшего поражения нервной системы, чем при короткой дуге, признак того, что блуждающий нерв раздражён по всей длине -H.B.)
Представим себе дугу с очень большим радиусом. Такую дугу - почти прямую линию, мы отнесем к норме, не имеющей патологии деформации и не склонной к прогрессированию, однако угол дуги, на условиях рис. 9, остается тем же, что и у дуги №6. Уменьшение угла этой дуги возможно лишь при уменьшении ее высоты, но никак не связано с реальной кривизной. Именно этот факт часто приводит к прямо противоположным выводам о прогрессировании или не прогрессировании дуги, которые делают врачи, основываясь на динамике угла Кобба.
На рис. 10 представлено три дуги А1 - А1', В1 - В1' и С1 - С1' равной высоты, но разной кривизны. Допустим, что это начальное состояние дуг трех различных пациентов. Нельзя не согласиться, что в процессе роста ребенка каждая из дуг может «сворачиваться» увеличивая кривизну, или наоборот - выправляться, в результате, например, чудодейственной корсетотерапии, уменьшая начальную кривизну.
При этом будет изменяться начальная высота дуги Н1 и начальные углы β1, β2, β3 соответственно поведению дуги. Но, нельзя также не согласиться, что в частном случае какая-то из дуг, например В1 - В1', может увеличиваться (расти) от Н1 до Н2 или Н3 не изменяя начальную кривизну.

Если дуга позвоночника В1 - В1' вырастет до состояния В2 - В2' (или В3 - В3'), то измеренный по Коббу угол также увеличиться до состояния β2′ (или β2''), хотя реальная кривизна дуги не изменилась.
Как отмечалось выше, не изменилась и степень патологичности дуги, т. е. не нарушилось ни геометрическое установившееся равновесие туловища, ни механическая устойчивость дуги к существующим силам и моментам сил - произошло лишь равномерное увеличение дуги (туловища), что характерно для любого здорового растущего организма. Но, врачом (рентгенологом) будет отмечено прогрессирование деформации на основании измерений по
Коббу. Мы неоднократно встречались с такими ошибочными заключениями.
Таким образом, параметр Кобба не выделяет причину изменения угла дуги: от изменения ее размера или от изменения реальной кривизны, поэтому он не может использоваться в качестве корректного оценочного параметра состояния дуги для растущего (организма). Тот же вывод следует и для частных случаев, например, для оценки эффекта коррекции деформации дуги в процессе корсетотерапии или коррекции путем оперативного
вмешательства.
Может показаться, что в интервале практических значений дуг представленные выше рассуждения не приводят к грубым ошибкам и можно поплатиться точностью измерений в угоду простоты рентгенологического обследования дуги. Отвечая на это замечание и забегая вперед, отметим, что это абсолютно неверно.
Теперь рассмотрим ситуацию с оценкой дуги по параметру кривизны. На рис. 11 изображено 6 дуг, максимально похожих на дуги по рис. 9, т.е., такой же высоты, но конкретной кривизны - 2 м‾¹, или, другими словами, это различные по длине дуги одного и того же радиуса (окружности). Дуга №2 на обоих рисунках в точности идентична, что отражено в таблице 2 под рисунком. Так же как и на рис. 9 дуга №4 имеет продление до c-d и ее можно сравнить с дугой №1 того же рисунка. Здесь нетрудно заметить, даже визуально, что обе дуги абсолютно схожи. Остальные - разные по высоте дуги, характеризуется, в данном случае, разными углами охвата.
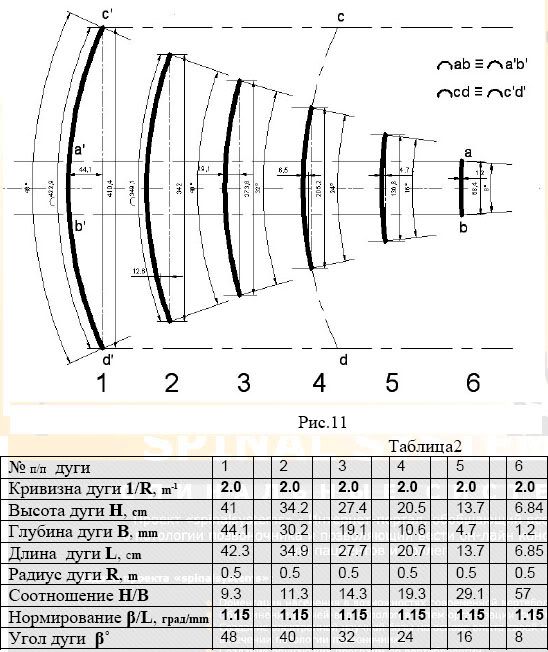
Для этого семейства дуг характерно либо равная кривизна, выраженная через радиус, либо равный относительный угол дуги, выраженный через соотношение угла и длины дуги - β/L. Это и есть база метода кривизны.
Продолжение: http://healthy-back.livejournal.com/156119.html