Das Эксперимент - 4: Схватка
Накопление достаточно большого экспериментального материала по первым тестам ("Точки", "Кружки", "Расстояния") дало возможность начать сравнение некоторых гипотез о виде основного психофизического закона и психометрической кривой.
Ход и результаты матчей
Фехнер против Стивенса
и
Гиперболический Тангенс против Функции Ошибок
можно узнать здесь!
Модель процесса сравнения, которую мы приняли, описыватся следующими постулатами.
I. Есть известная величина стимула (например, истинное число точек на рисунке). От нее зависит субъективная величина стимула ("сила ощущения").
II. Сравнение двух стимулов может приводить к трем типам результатов: первый стимул больше, одинаково, второй стимул больше. Каждый результат сравнения имеет свою вероятность (в сумме три вероятности равны 1).
III. Все три вероятностями являются некоторыми функциями от разности значений субъективной величины сравниваемых стимулов.
Для того, чтобы такая модель полность описывала процесс сравнения, в ней необходимо задать два типа функций, которые показывают:
1) как именно субъективная величина стимула зависит от его объективной величины - эта функция назывется основным психофизическим законом;
2) как именно вероятность данного варианта ответа зависит от разности субъективных величин стимулов - это так называемая психометрическая кривая для дифференциального порога.
Особенность модели в том, психометрическая кривая берется как функция разности субъективных (а не объективных) величин стимулов - вместе с постулатом III это позволяет использовать для оценки психометрической кривой все результаты сравнений, а не только результаты, в которых величина одного из стимулов фиксирована.
Первый этап исследования состоит в том, чтобы принять некоторое разумное предположение о виде основного психофизического закона, и в этом предположении по экспериментальным данным узнать психофизическую кривую. (После этого вид основного психофизического закона можно будет уточнить.)
Существуют две версии основного психофизического закона. Исторически первая была предложена в 1860 г. Г.Т.Фехнером, она заключается в логарифмической зависимости силы ощущения от величины стимула
f(x) = k ln(x/xt),
здесь x - стимул, f - ощущение, xt - пороговое (минимальное) значение стимула.
Альтернативный вариант был предложен в 1961 г. С.С.Стивенсом. Он предполагает степенной вид этой зависимости
f(x) = k (x-xt)n,
где степень n не является целой и может изменяться в широких пределах в зависимости от типа стимула.
Есть еще более сложный вариант Ю.М.Забродина, который включает оба этих закона в качестве частных случаев и, соответственно, содержит еще одну дополнительную константу.
В качестве стартовой гипотезы о виде основного психофизического закона мы выбрали вариант Фехнера, как имеющий более долгую историю эмпирической проверки и, главное, как более простой - в случае использования закона Стивенса нужно знать показатель степени, который сильно зависит от природы стимула, и его было бы затруднительно задать заранее.
Итак, на первом шаге мы смотрим, как вероятности трех вариантов ответов зависят от разности логарифмов (закон Фехнера) стимулов. На данный момент оценки кривых вероятностей по экспериментальным данным (по всем участникам, не более двух тестов на каждого участника) выглядят следующим образом.
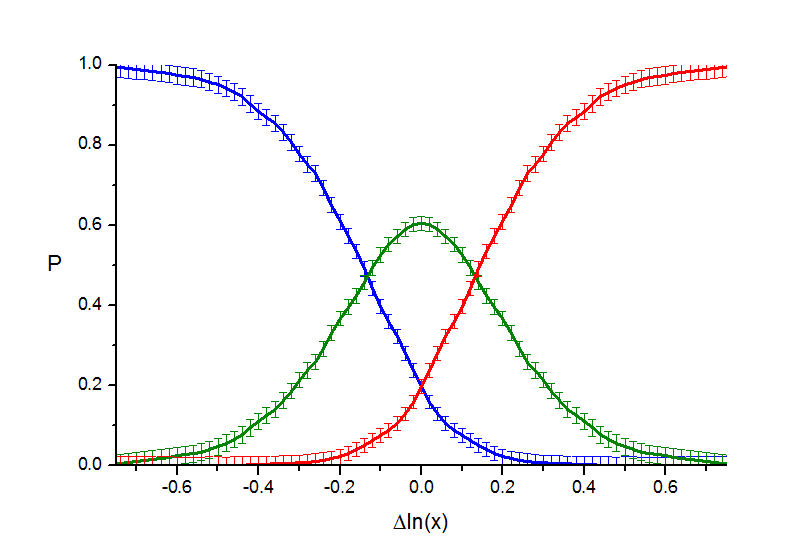
Рис. 1.1. "Точки" - 392 испытуемых, 437 экспериментов. Кривые вероятности.
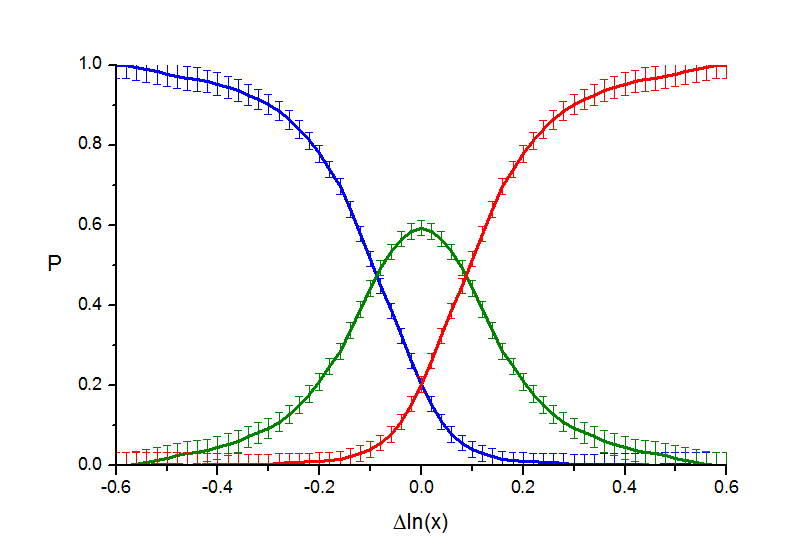
Рис. 1.2. "Кружки" - 179 испытуемых, 196 экспериментов. Кривые вероятности.
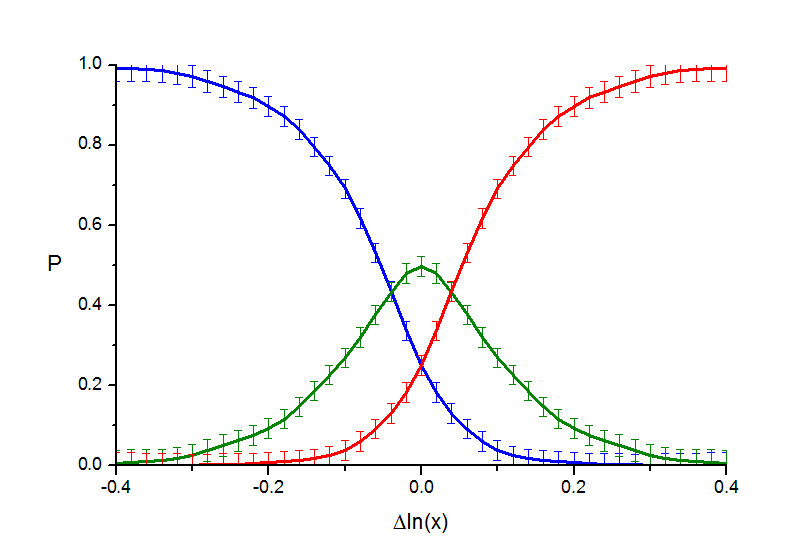
Рис. 1.3. "Расстояния" - 95 испытуемых, 106 экспериментов. Кривые вероятности.
Кривые достаточно плавные, не содержат изломов или других особенностей. Первая версия - что это логистические кривые (получаемые из гиперболического тангенса, th(x); так, вероятность того, что второй стимул больше - 0.5(1+th((y-a)/2d), где y - разность логарифмов стимулов). В этом предположении о виде кривых параметры сдвига a и ширины d были найдены по экспериментальным данным исходя их принципа максимального правдоподобия. Насколько эти кривые согласуются с эмпирическими видно на следующих рисунках:
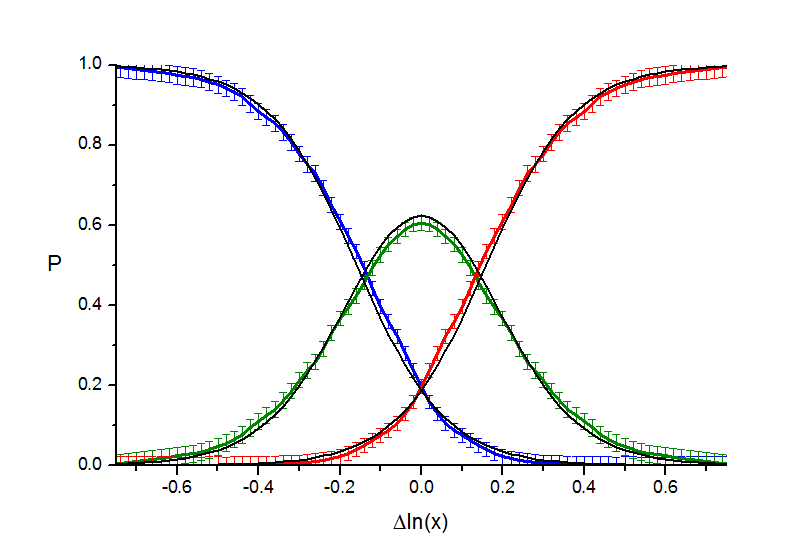
Рис. 2.1. "Точки". Аппроксимация кривых вероятности гиперболическим тангенсом.
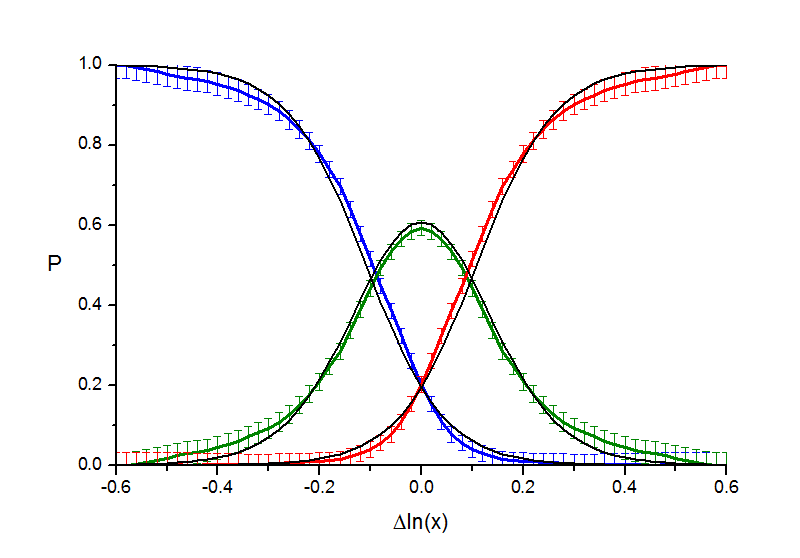
Рис. 2.2. "Кружки". Аппроксимация кривых вероятности гиперболическим тангенсом.
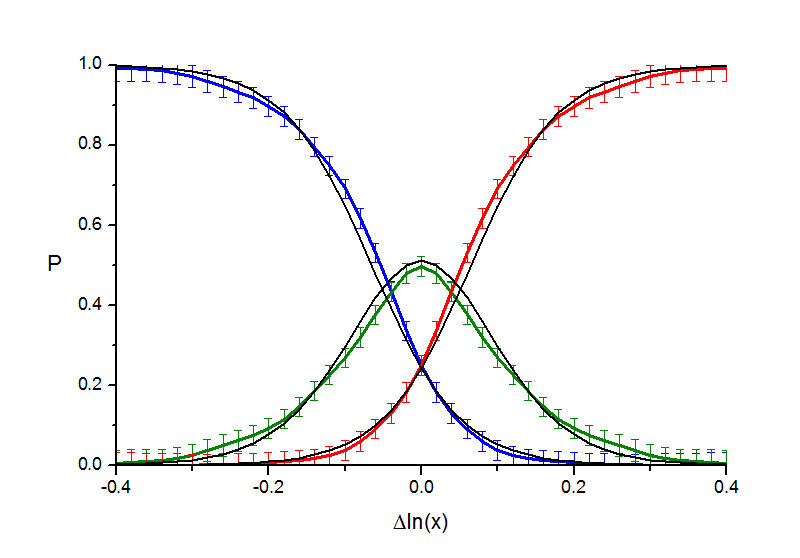
Рис. 2.3. "Расстояния". Аппроксимация кривых вероятности гиперболическим тангенсом.
Альтернативная гипотеза о форме кривых вероятностей заключается в том, что они соответствуют функции распределения для гауссовского закона, т.е. вместо гиперболического тангенса выражаются через функцию ошибок erf(x). Именно эта гипотеза обычно принимается в психофизике (ей противопоставляют предположение о кусочно-линейном характере психофизической кривой, но, очевидно, в нашем случае кусочная линейность не согласуется с экспериментальными данными). Этот вариант также был нами рассмотрен, его иллюстрирует следующая серия рисунков.
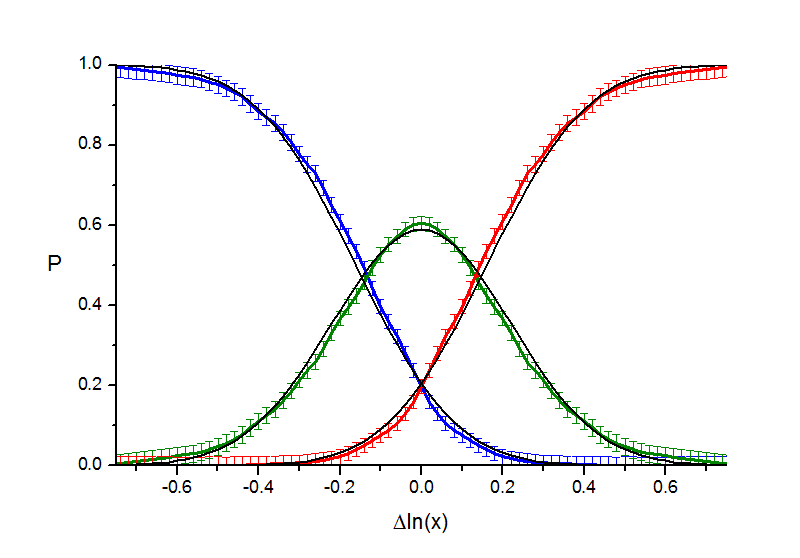
Рис. 3.1. "Точки". Аппроксимация кривых вероятности функцией ошибок.
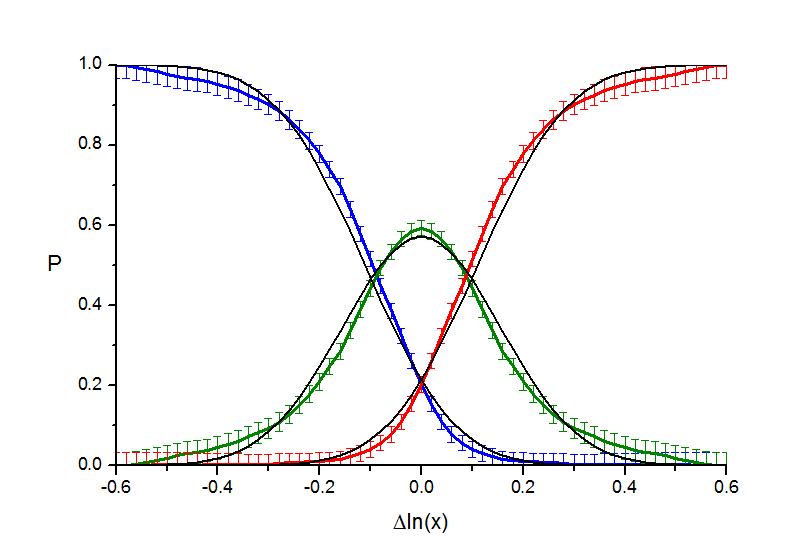
Рис. 3.2. "Кружки". Аппроксимация кривых вероятности функцией ошибок.
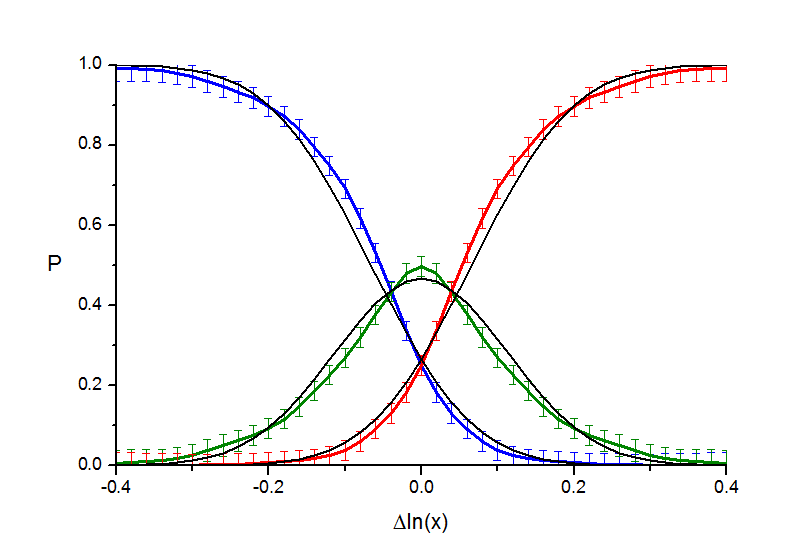
Рис. 3.3. "Расстояния". Аппроксимация кривых вероятности функцией ошибок.
Из рисунков видно, что:
1. Обе гипотезы (th(x) и erf(x)) соответсвуют качественным особенностям кривых (плавный ход без изломов и других особенностей). В то же время, есть небольшие количественные расхождения (более заметные в тестах "кружки" и "расстояния").
2. Для функции ошибок erf(x) отклонения несколько больше.
После первого раунда с небольшим преимуществом лидирует гиперболический тангенс.
На втором этапе исследования, аналитически задав вид кривых вероятности, мы переходим к обратной задаче - определить субъективную величину стимула как функцию его объективной величины, т.е. теперь уже непосредственно из эмпирических данных получить вид психофизического закона.
Параметры a и d кривых вероятности при решении обратной задачи выбирались из следующих соображений. Параметр d фиксировался так, чтобы максимальное значение производной психометрической кривой было равным 1. (Величину, обратную производной, мы здесь принимаем за ширину порога, таким образом ширина порога тоже равна 1, т.е. в результате психофизический закон будет выражен в единицах таким образом заданной ширины порога.) Параметр a выбирался из соображений наилучшего соответствия экспериментальным данным.
Приведем получившися кривые f(x) для обоих вариантов выбора психометрических кривых - на основе th(x) и на основе erf(x).
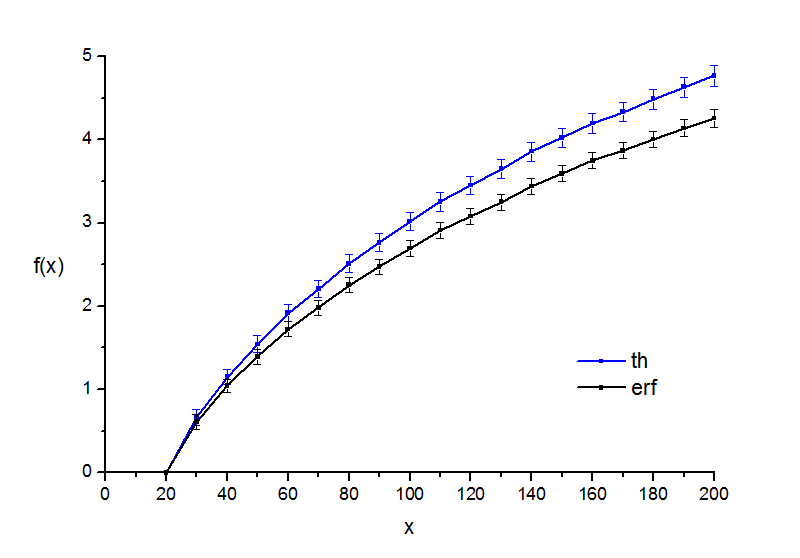
Рис. 4.1. "Точки". Вид полученного психофизического закона.
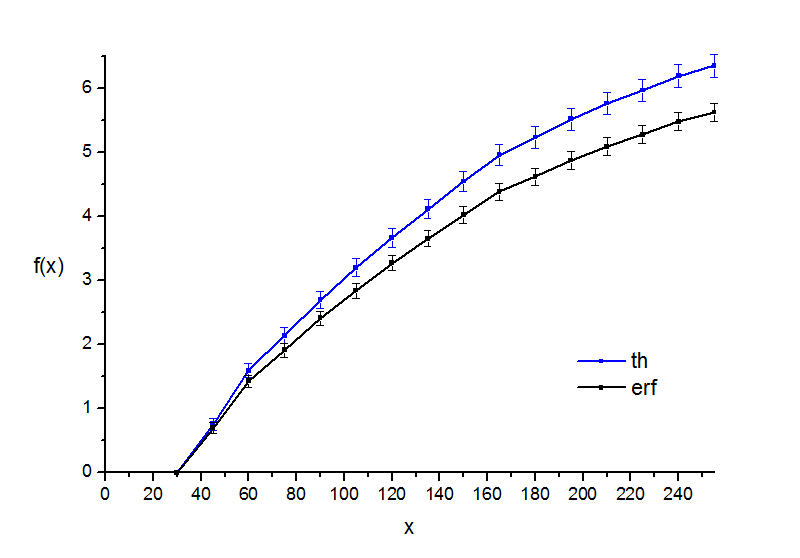
Рис. 4.2. "Кружки". Вид полученного психофизического закона.
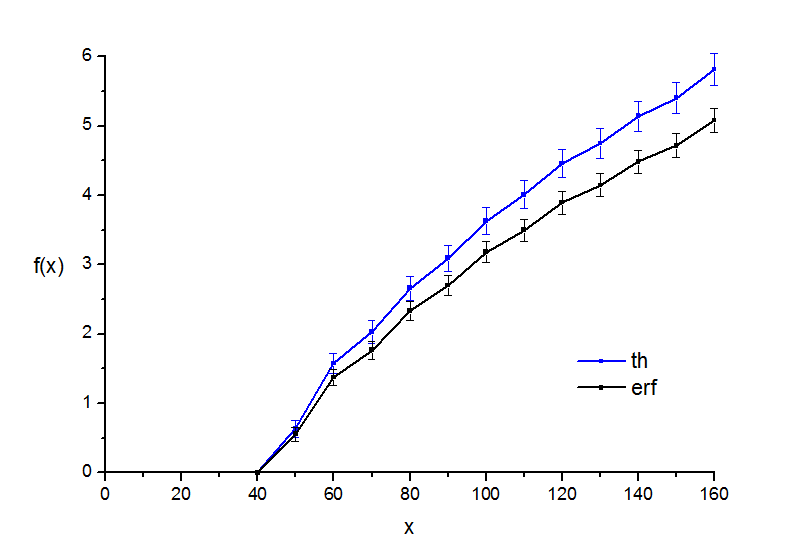
Рис. 4.3. "Расстояния". Вид полученного психофизического закона.
Видно, что на сам ход зависимостей разница в вариантах выбора кривых вероятности практически не влияет, слегка меняется лишь эффективная величина порога, т.е. единица измерения. Наиболее гладкая кривая получается там, где больше всего данных, т.е. в эксперименте с точками.
То, что кривые f(x) получились практически одинаковыми по форме, свидетельствует о том, что существенной практической разницы между двумя гипотезами о форме психофизической кривой нет.
Гипеболический тангенс уменьшает свое преимущество по очкам.
Теперь посмотрим, что же получилось, какой вид психофизического закона наилучшим образом соответствует полученным зависимостям. Попробуем аппроксимировать ее различными формами психофизического закона.
1. В исходном виде закон Фехнера (логарифм - f(x) = k ln(x/xt)) дает достаточно грубую аппроксимацию (зеленая кривая на рисунках) - при качественном совпадение (монотонный рост, выпуклость вверх) количественные расхождения достигают 0.25 пороговых единиц.
(Здесь и далее xt - это, по смыслу, минимальное значение стимула, используемое в эксперименте. Его вхождение в формулы обеспечивает необходимый сдвиг по оси абсцисс, так как экспериментальные кривые "по построению" выходят из нуля в точке минимального значения стимула - ведь мы можем оценить только изменения субъективной величины стимула, а не ее абсолютное значение, и вынуждены использовать нормировку, в качестве которой взят ноль субъективной величины стимула на нижней границе области изменения объективной величины стимула.)
2. Для уменьшения этого расхождения мы добавили в закон Фехнера дополнительный параметр - сдвиг начала координат x0:
f(x) = k ln((x-x0)/(xt-x0)).
Это красная кривая на графиках. В таком варианте расхождение с эмпирической оценкой оказывается на порядок меньше и лежит в пределах погрешности эксперимента.
3. Закон Стивенса в виде f(x) = k (xn-xtn) также дает совпадение с эмпирической оценкой в пределах погрешности эксперимента (Это синяя кривая на графиках). Показатель степени n для каждого из трех экспериментов свой, но во всех случаях его значения лежат в интервале от 0.2 до 0.3.
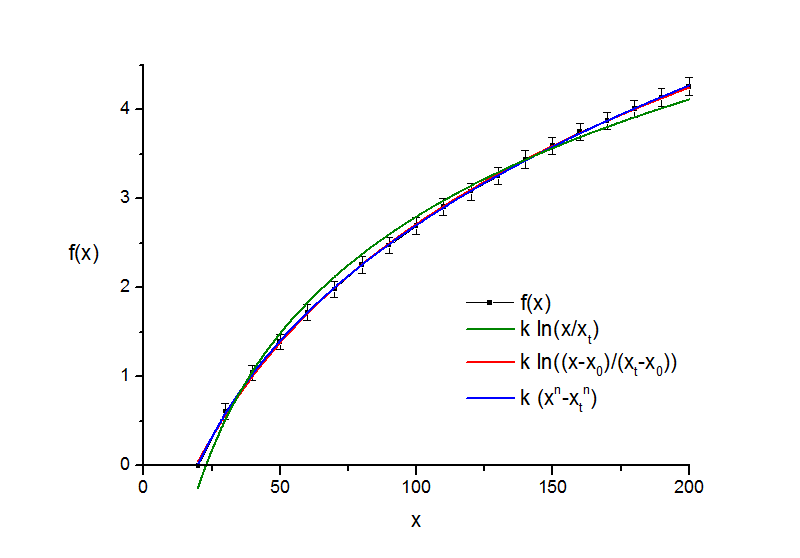
Рис. 5.1. "Точки". Аппроксимация полученного психофизического закона.
x0=-24.6+1.7, n=0.269+0.007

Рис. 5.2. "Кружки". Аппроксимация полученного психофизического закона.
x0=-37.1+5.7, n=0.279+0.037
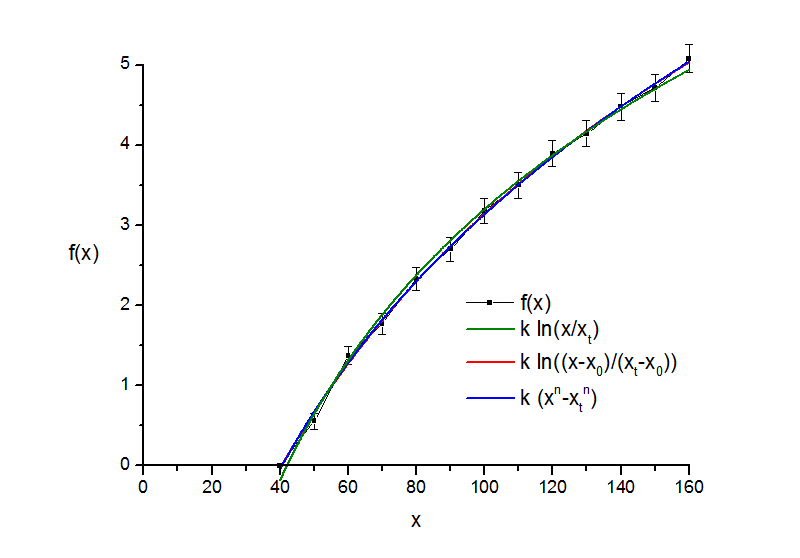
Рис. 5.3. "Расстояния". Аппроксимация полученного психофизического закона.
x0=-23.2+7.7, n=0.223+0.056
В итоге результат такой: "чистый" Фехнер проигрывает Стивенсу, а Фехнер со сдвинутым началом координат дает такое же хорошее соответствие экспериментальным результатам. (На рисунках красная и синяя кривые практически совпадают.)
Ничья.
Сдвиг начала координат x0 во всех случаях отрицательный имеет тот же порядок величины, что и минимальное значение стимула, использованное в эксперименте.
Теперь, когда у нас есть экспериментально определенная форма основного психофизического закона, мы можем вернуться к сравнению психофизических кривых и уточнить его результаты (исключив погрешности, которые вносила недостаточно точная стартовая гипотеза о виде психофизического закона). Если теперь построить кривые вероятностей как функции разности субъектиных величин стимулов, то для двух рассморенных вариантов получатся следующие картины:
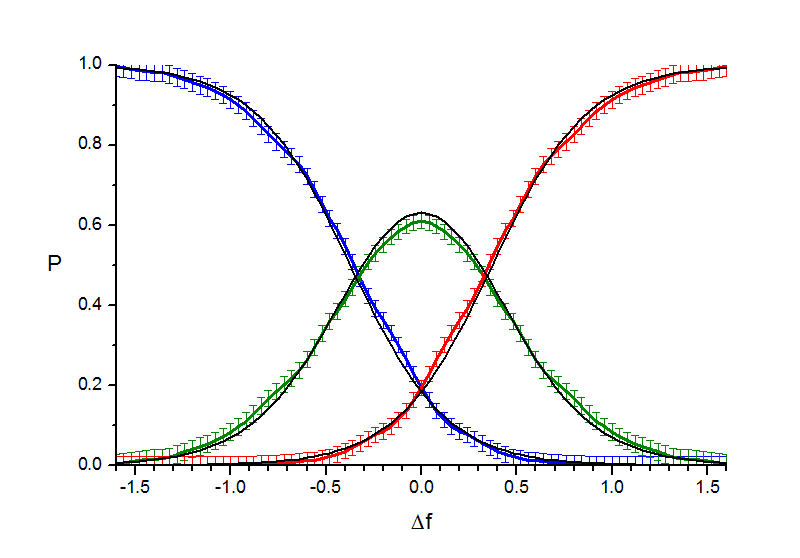
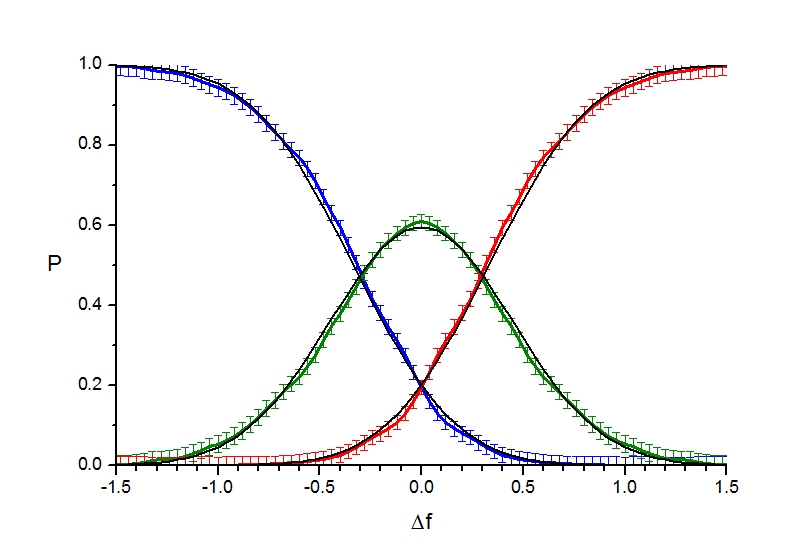
а) th(x)б) erf(x)
Рис. 6.1. "Точки". Аппроксимация кривых вероятности.

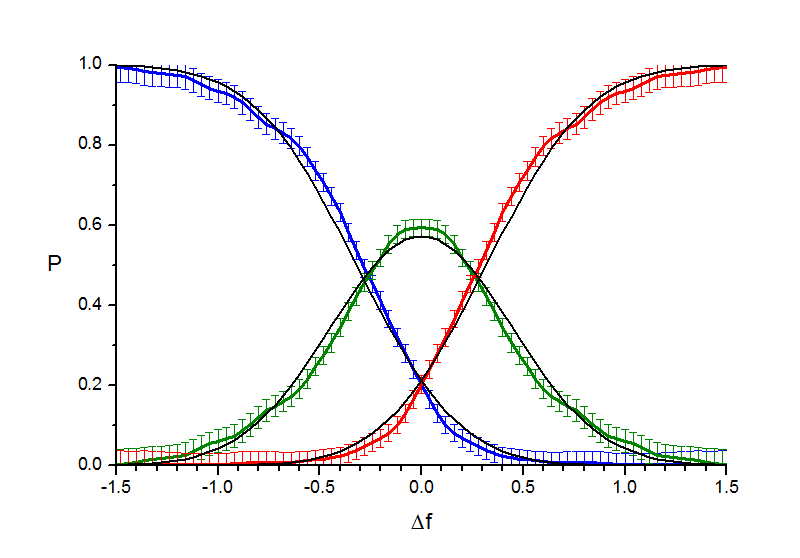
а) th(x)б) erf(x)
Рис. 6.2. "Кружки". Аппроксимация кривых вероятности.
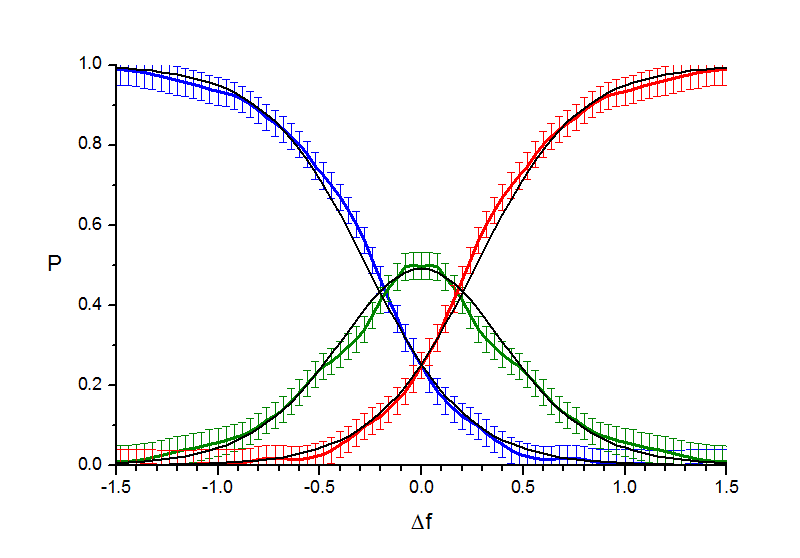

а) th(x)б) erf(x)
Рис. 6.3. "Расстояния" Аппроксимация кривых вероятности.
Можно видеть, что согласованность экспериментальных кривых с теоретическими слегка улучшилась. Для эксперимета с точками, по которому есть наибольшее количество данных, эта согласованность наиболее полная. Что касается выбора между гиперболическим тангенсом и функцией ошибок, то его по прежнему нельзя однозначно сделать, хотя для эксперимента с точками теперь не гиперболический тангенс, а функция ошибок дает чуть лучшее приближение (для двух других экспериментов результаты приблизительно одинаковы).
Итак, обе партии завершилиь вничью.
По итогам можно сделать следующие выводы.
1. Закон Фехнера со смещенным началом координат и закон Стивенса оба хорошо согласутся с экспериментальными данными.
2. Для кривых вероятности аналитические модели, основанные на th(x) и erf(x), обе дают удовлетворительные результаты.
3. В целом предложенная модель проявила высокую работоспособность и ее можно использовать в дальнейшем.
Продолжение следует. По эстетическим тестам есть интересные наблюдения, однако по двум последним тестам - с абстрактными картинами - еще набралось недостаточно данных. Поэтому большая просьба - пройдите тесты с абстрактными картинами еще раз.
http://kinoseminar.ru/aesthetics/index.php
Также мы ждем предложений по новым эстетическим тестам.
Ход и результаты матчей
Фехнер против Стивенса
и
Гиперболический Тангенс против Функции Ошибок
можно узнать здесь!
Модель процесса сравнения, которую мы приняли, описыватся следующими постулатами.
I. Есть известная величина стимула (например, истинное число точек на рисунке). От нее зависит субъективная величина стимула ("сила ощущения").
II. Сравнение двух стимулов может приводить к трем типам результатов: первый стимул больше, одинаково, второй стимул больше. Каждый результат сравнения имеет свою вероятность (в сумме три вероятности равны 1).
III. Все три вероятностями являются некоторыми функциями от разности значений субъективной величины сравниваемых стимулов.
Для того, чтобы такая модель полность описывала процесс сравнения, в ней необходимо задать два типа функций, которые показывают:
1) как именно субъективная величина стимула зависит от его объективной величины - эта функция назывется основным психофизическим законом;
2) как именно вероятность данного варианта ответа зависит от разности субъективных величин стимулов - это так называемая психометрическая кривая для дифференциального порога.
Особенность модели в том, психометрическая кривая берется как функция разности субъективных (а не объективных) величин стимулов - вместе с постулатом III это позволяет использовать для оценки психометрической кривой все результаты сравнений, а не только результаты, в которых величина одного из стимулов фиксирована.
Первый этап исследования состоит в том, чтобы принять некоторое разумное предположение о виде основного психофизического закона, и в этом предположении по экспериментальным данным узнать психофизическую кривую. (После этого вид основного психофизического закона можно будет уточнить.)
Существуют две версии основного психофизического закона. Исторически первая была предложена в 1860 г. Г.Т.Фехнером, она заключается в логарифмической зависимости силы ощущения от величины стимула
f(x) = k ln(x/xt),
здесь x - стимул, f - ощущение, xt - пороговое (минимальное) значение стимула.
Альтернативный вариант был предложен в 1961 г. С.С.Стивенсом. Он предполагает степенной вид этой зависимости
f(x) = k (x-xt)n,
где степень n не является целой и может изменяться в широких пределах в зависимости от типа стимула.
Есть еще более сложный вариант Ю.М.Забродина, который включает оба этих закона в качестве частных случаев и, соответственно, содержит еще одну дополнительную константу.
В качестве стартовой гипотезы о виде основного психофизического закона мы выбрали вариант Фехнера, как имеющий более долгую историю эмпирической проверки и, главное, как более простой - в случае использования закона Стивенса нужно знать показатель степени, который сильно зависит от природы стимула, и его было бы затруднительно задать заранее.
Итак, на первом шаге мы смотрим, как вероятности трех вариантов ответов зависят от разности логарифмов (закон Фехнера) стимулов. На данный момент оценки кривых вероятностей по экспериментальным данным (по всем участникам, не более двух тестов на каждого участника) выглядят следующим образом.

Рис. 1.1. "Точки" - 392 испытуемых, 437 экспериментов. Кривые вероятности.

Рис. 1.2. "Кружки" - 179 испытуемых, 196 экспериментов. Кривые вероятности.

Рис. 1.3. "Расстояния" - 95 испытуемых, 106 экспериментов. Кривые вероятности.
Кривые достаточно плавные, не содержат изломов или других особенностей. Первая версия - что это логистические кривые (получаемые из гиперболического тангенса, th(x); так, вероятность того, что второй стимул больше - 0.5(1+th((y-a)/2d), где y - разность логарифмов стимулов). В этом предположении о виде кривых параметры сдвига a и ширины d были найдены по экспериментальным данным исходя их принципа максимального правдоподобия. Насколько эти кривые согласуются с эмпирическими видно на следующих рисунках:

Рис. 2.1. "Точки". Аппроксимация кривых вероятности гиперболическим тангенсом.

Рис. 2.2. "Кружки". Аппроксимация кривых вероятности гиперболическим тангенсом.

Рис. 2.3. "Расстояния". Аппроксимация кривых вероятности гиперболическим тангенсом.
Альтернативная гипотеза о форме кривых вероятностей заключается в том, что они соответствуют функции распределения для гауссовского закона, т.е. вместо гиперболического тангенса выражаются через функцию ошибок erf(x). Именно эта гипотеза обычно принимается в психофизике (ей противопоставляют предположение о кусочно-линейном характере психофизической кривой, но, очевидно, в нашем случае кусочная линейность не согласуется с экспериментальными данными). Этот вариант также был нами рассмотрен, его иллюстрирует следующая серия рисунков.

Рис. 3.1. "Точки". Аппроксимация кривых вероятности функцией ошибок.

Рис. 3.2. "Кружки". Аппроксимация кривых вероятности функцией ошибок.

Рис. 3.3. "Расстояния". Аппроксимация кривых вероятности функцией ошибок.
Из рисунков видно, что:
1. Обе гипотезы (th(x) и erf(x)) соответсвуют качественным особенностям кривых (плавный ход без изломов и других особенностей). В то же время, есть небольшие количественные расхождения (более заметные в тестах "кружки" и "расстояния").
2. Для функции ошибок erf(x) отклонения несколько больше.
После первого раунда с небольшим преимуществом лидирует гиперболический тангенс.
На втором этапе исследования, аналитически задав вид кривых вероятности, мы переходим к обратной задаче - определить субъективную величину стимула как функцию его объективной величины, т.е. теперь уже непосредственно из эмпирических данных получить вид психофизического закона.
Параметры a и d кривых вероятности при решении обратной задачи выбирались из следующих соображений. Параметр d фиксировался так, чтобы максимальное значение производной психометрической кривой было равным 1. (Величину, обратную производной, мы здесь принимаем за ширину порога, таким образом ширина порога тоже равна 1, т.е. в результате психофизический закон будет выражен в единицах таким образом заданной ширины порога.) Параметр a выбирался из соображений наилучшего соответствия экспериментальным данным.
Приведем получившися кривые f(x) для обоих вариантов выбора психометрических кривых - на основе th(x) и на основе erf(x).

Рис. 4.1. "Точки". Вид полученного психофизического закона.

Рис. 4.2. "Кружки". Вид полученного психофизического закона.

Рис. 4.3. "Расстояния". Вид полученного психофизического закона.
Видно, что на сам ход зависимостей разница в вариантах выбора кривых вероятности практически не влияет, слегка меняется лишь эффективная величина порога, т.е. единица измерения. Наиболее гладкая кривая получается там, где больше всего данных, т.е. в эксперименте с точками.
То, что кривые f(x) получились практически одинаковыми по форме, свидетельствует о том, что существенной практической разницы между двумя гипотезами о форме психофизической кривой нет.
Гипеболический тангенс уменьшает свое преимущество по очкам.
Теперь посмотрим, что же получилось, какой вид психофизического закона наилучшим образом соответствует полученным зависимостям. Попробуем аппроксимировать ее различными формами психофизического закона.
1. В исходном виде закон Фехнера (логарифм - f(x) = k ln(x/xt)) дает достаточно грубую аппроксимацию (зеленая кривая на рисунках) - при качественном совпадение (монотонный рост, выпуклость вверх) количественные расхождения достигают 0.25 пороговых единиц.
(Здесь и далее xt - это, по смыслу, минимальное значение стимула, используемое в эксперименте. Его вхождение в формулы обеспечивает необходимый сдвиг по оси абсцисс, так как экспериментальные кривые "по построению" выходят из нуля в точке минимального значения стимула - ведь мы можем оценить только изменения субъективной величины стимула, а не ее абсолютное значение, и вынуждены использовать нормировку, в качестве которой взят ноль субъективной величины стимула на нижней границе области изменения объективной величины стимула.)
2. Для уменьшения этого расхождения мы добавили в закон Фехнера дополнительный параметр - сдвиг начала координат x0:
f(x) = k ln((x-x0)/(xt-x0)).
Это красная кривая на графиках. В таком варианте расхождение с эмпирической оценкой оказывается на порядок меньше и лежит в пределах погрешности эксперимента.
3. Закон Стивенса в виде f(x) = k (xn-xtn) также дает совпадение с эмпирической оценкой в пределах погрешности эксперимента (Это синяя кривая на графиках). Показатель степени n для каждого из трех экспериментов свой, но во всех случаях его значения лежат в интервале от 0.2 до 0.3.

Рис. 5.1. "Точки". Аппроксимация полученного психофизического закона.
x0=-24.6+1.7, n=0.269+0.007

Рис. 5.2. "Кружки". Аппроксимация полученного психофизического закона.
x0=-37.1+5.7, n=0.279+0.037

Рис. 5.3. "Расстояния". Аппроксимация полученного психофизического закона.
x0=-23.2+7.7, n=0.223+0.056
В итоге результат такой: "чистый" Фехнер проигрывает Стивенсу, а Фехнер со сдвинутым началом координат дает такое же хорошее соответствие экспериментальным результатам. (На рисунках красная и синяя кривые практически совпадают.)
Ничья.
Сдвиг начала координат x0 во всех случаях отрицательный имеет тот же порядок величины, что и минимальное значение стимула, использованное в эксперименте.
Теперь, когда у нас есть экспериментально определенная форма основного психофизического закона, мы можем вернуться к сравнению психофизических кривых и уточнить его результаты (исключив погрешности, которые вносила недостаточно точная стартовая гипотеза о виде психофизического закона). Если теперь построить кривые вероятностей как функции разности субъектиных величин стимулов, то для двух рассморенных вариантов получатся следующие картины:


а) th(x)б) erf(x)
Рис. 6.1. "Точки". Аппроксимация кривых вероятности.


а) th(x)б) erf(x)
Рис. 6.2. "Кружки". Аппроксимация кривых вероятности.


а) th(x)б) erf(x)
Рис. 6.3. "Расстояния" Аппроксимация кривых вероятности.
Можно видеть, что согласованность экспериментальных кривых с теоретическими слегка улучшилась. Для эксперимета с точками, по которому есть наибольшее количество данных, эта согласованность наиболее полная. Что касается выбора между гиперболическим тангенсом и функцией ошибок, то его по прежнему нельзя однозначно сделать, хотя для эксперимента с точками теперь не гиперболический тангенс, а функция ошибок дает чуть лучшее приближение (для двух других экспериментов результаты приблизительно одинаковы).
Итак, обе партии завершилиь вничью.
По итогам можно сделать следующие выводы.
1. Закон Фехнера со смещенным началом координат и закон Стивенса оба хорошо согласутся с экспериментальными данными.
2. Для кривых вероятности аналитические модели, основанные на th(x) и erf(x), обе дают удовлетворительные результаты.
3. В целом предложенная модель проявила высокую работоспособность и ее можно использовать в дальнейшем.
Продолжение следует. По эстетическим тестам есть интересные наблюдения, однако по двум последним тестам - с абстрактными картинами - еще набралось недостаточно данных. Поэтому большая просьба - пройдите тесты с абстрактными картинами еще раз.
http://kinoseminar.ru/aesthetics/index.php
Также мы ждем предложений по новым эстетическим тестам.