Магнитный парус наносит ответный удар
В прошлом посте было рассказано, что пучок заряженных частиц не может существовать потому, что его расталкивают кулоновские силы. Но что если я вам скажу, что уравнений Максвелла больше одного?

В прошлом посте мы использовали исключительно теорему Гаусса. Электрические заряды создают электрическое поле, которое отталкивает другие заряды. Поэтому много одноименно заряженных частиц не могут находиться рядом. Или все же могут?
Что если я вам скажу, что параллельные проводники, ток в которых сонаправлен, притягиваются?

Собственно, кроме теоремы Гаусса есть обобщенный закон Био-Савара-Лапласа, говорящий о том, что ток создает магнитное поле. А ток это ни что иное как движение зарядов. То есть, пучок заряженных частиц это ток с плотностью j. И наша условная частица на краю пучка тоже представляет собой ток. И на нее действует сила Лоренца, полностью аналогичная по генезису силе Ампера.
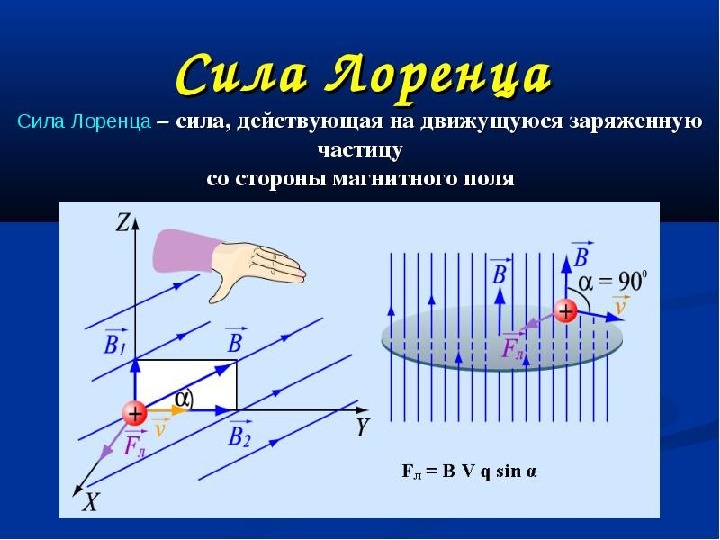
В однородном магнитном поле частица будет двигаться по кругу, что и используется в кольцевых ускорителях. Но поле бесконечного прямого проводника с током в свою очередь закольцованное.

Куда в нем будет направлена сила Лоренца? К центру или от центра в зависимости от заряда частицы, ровно так же, как сила Ампера. Итак, положительно заряженная частица, летящая вдоль проводника в направлении, совпадающем с направлением тока, будет притягиваться к нему.
При наличии двух противонаправленных сил неизбежно возникает вопрос об их численном соотношении.

Обозначения аналогичны предыдущему посту, плюс появилась магнитная постоянная мю-ноль. От плотности заряда сигма мы перешли к заряду q, протекающему сечение нашего условного проводника за единицу времени, чтобы привести к одинаковым физическим величинам. В прошлый раз можно было заметить, что числа в Кл*моль/с соответствую как раз плотности тока А*моль.
Теперь к сути. Во-первых, сила Кулона обратно пропорциональна квадрату расстояния до оси пучка, а сила Лоренца - первой степени. Из чего следует существование такого значения r, при котором сила Кулона уступает силе Лоренца, условная частица на краю больше не испытывает неудержимой тяги оказаться подальше от этих идиотов, и пучок самофокусируется. Во-вторых, обе силы пропорциональны первой степени как заряда частицы, так и плотности заряда пучка. То есть, это значение r не зависит ни от того, какие частицы, ни от того, сколько их. Лишь бы были одноименно заряженные.

Люблю запах сведения к фундаментальным константам по утрам. Это запах победы. Разумеется, скорость света там возникла не случайно, а из фундаментального соотношения электрической и магнитной постоянных, которое следует из уравнений Максвелла, которых больше одного.
Итак, положение устойчивого равновесия частицы в электромагнитном поле движущегося пучка имеет вид цилиндра с осью, соответствующей оси пучка, и радиусом, равным произведению пяти сантиметров на квадрат отношения скорости света к скорости пучка. Разумеется, реальные частицы будут "гулять" вокруг этого положения под воздействием других факторов, и в целом у нас получится цилиндр с радиусом, несколько превышающим r_e, но имеющим тот же порядок величины. Так или иначе, стабильный радиус пучка, претендующего на звание релятивистского, 10 метров превышать не будет. И тут уже проблема не собрать энергию парусом, а центрировать пучок на парусе.
Кстати, здесь же видна проблема с нейтрализованными пучками. Идеальной нейтрализации достичь не получится, у пучка всегда будет "остаточная" плотность заряда, которая имеет знак. Если она положительная, то отдрейфовавшие на границу пучка протоны попадают в устойчивое равновесие, а вот электроны - в неустойчивое. Т.е., стремительно улетучиваются из пучка. Так что, предельная дальность ускорительной пушки с нейтрализацией (а другой не будет, радиус пучка порядка десятков сантиметров совершенно непригоден для пушки) определяется уже уравнениями теплового движения электронов.
Конечно, итоговый ответ является удивительным. Поэтому эту часть вычислений я сначала отправил проверенным камрадам. Получив ответ, что все так, публикую. Если кто-то из читателей расскажет мне в комментариях, где я ошибся, - буду очень признателен. Если нет, то через неделю опубликую расчеты и в АТ.

В прошлом посте мы использовали исключительно теорему Гаусса. Электрические заряды создают электрическое поле, которое отталкивает другие заряды. Поэтому много одноименно заряженных частиц не могут находиться рядом. Или все же могут?
Что если я вам скажу, что параллельные проводники, ток в которых сонаправлен, притягиваются?

Собственно, кроме теоремы Гаусса есть обобщенный закон Био-Савара-Лапласа, говорящий о том, что ток создает магнитное поле. А ток это ни что иное как движение зарядов. То есть, пучок заряженных частиц это ток с плотностью j. И наша условная частица на краю пучка тоже представляет собой ток. И на нее действует сила Лоренца, полностью аналогичная по генезису силе Ампера.

В однородном магнитном поле частица будет двигаться по кругу, что и используется в кольцевых ускорителях. Но поле бесконечного прямого проводника с током в свою очередь закольцованное.

Куда в нем будет направлена сила Лоренца? К центру или от центра в зависимости от заряда частицы, ровно так же, как сила Ампера. Итак, положительно заряженная частица, летящая вдоль проводника в направлении, совпадающем с направлением тока, будет притягиваться к нему.
При наличии двух противонаправленных сил неизбежно возникает вопрос об их численном соотношении.

Обозначения аналогичны предыдущему посту, плюс появилась магнитная постоянная мю-ноль. От плотности заряда сигма мы перешли к заряду q, протекающему сечение нашего условного проводника за единицу времени, чтобы привести к одинаковым физическим величинам. В прошлый раз можно было заметить, что числа в Кл*моль/с соответствую как раз плотности тока А*моль.
Теперь к сути. Во-первых, сила Кулона обратно пропорциональна квадрату расстояния до оси пучка, а сила Лоренца - первой степени. Из чего следует существование такого значения r, при котором сила Кулона уступает силе Лоренца, условная частица на краю больше не испытывает неудержимой тяги оказаться подальше от этих идиотов, и пучок самофокусируется. Во-вторых, обе силы пропорциональны первой степени как заряда частицы, так и плотности заряда пучка. То есть, это значение r не зависит ни от того, какие частицы, ни от того, сколько их. Лишь бы были одноименно заряженные.

Люблю запах сведения к фундаментальным константам по утрам. Это запах победы. Разумеется, скорость света там возникла не случайно, а из фундаментального соотношения электрической и магнитной постоянных, которое следует из уравнений Максвелла, которых больше одного.
Итак, положение устойчивого равновесия частицы в электромагнитном поле движущегося пучка имеет вид цилиндра с осью, соответствующей оси пучка, и радиусом, равным произведению пяти сантиметров на квадрат отношения скорости света к скорости пучка. Разумеется, реальные частицы будут "гулять" вокруг этого положения под воздействием других факторов, и в целом у нас получится цилиндр с радиусом, несколько превышающим r_e, но имеющим тот же порядок величины. Так или иначе, стабильный радиус пучка, претендующего на звание релятивистского, 10 метров превышать не будет. И тут уже проблема не собрать энергию парусом, а центрировать пучок на парусе.
Кстати, здесь же видна проблема с нейтрализованными пучками. Идеальной нейтрализации достичь не получится, у пучка всегда будет "остаточная" плотность заряда, которая имеет знак. Если она положительная, то отдрейфовавшие на границу пучка протоны попадают в устойчивое равновесие, а вот электроны - в неустойчивое. Т.е., стремительно улетучиваются из пучка. Так что, предельная дальность ускорительной пушки с нейтрализацией (а другой не будет, радиус пучка порядка десятков сантиметров совершенно непригоден для пушки) определяется уже уравнениями теплового движения электронов.
Конечно, итоговый ответ является удивительным. Поэтому эту часть вычислений я сначала отправил проверенным камрадам. Получив ответ, что все так, публикую. Если кто-то из читателей расскажет мне в комментариях, где я ошибся, - буду очень признателен. Если нет, то через неделю опубликую расчеты и в АТ.