Ключи от портала?
Изображения с энциклопедий.
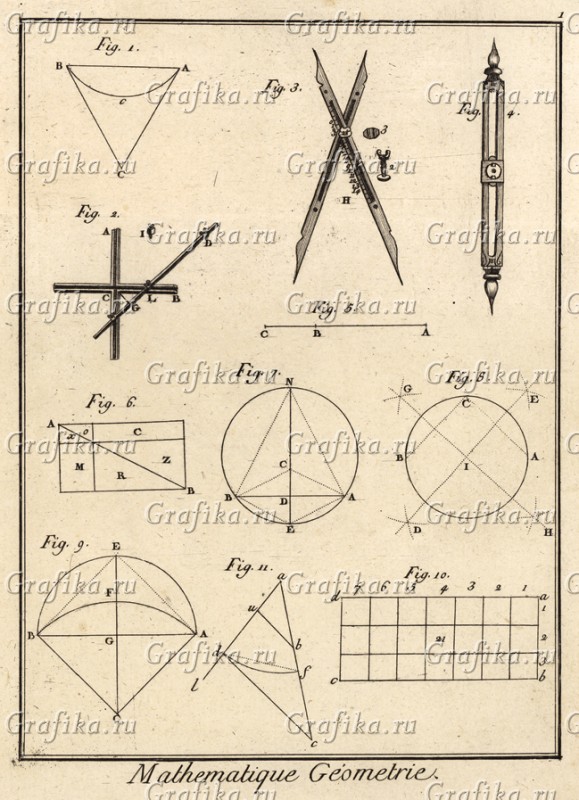
Mathematique Geometrie рис1: Работа с пропорциями, как минимум 3 прибора, где fig.3 вроде как циркуль? Но что-то в нём смущает? А! Это пропорциональный циркуль! У него «гвоздик» переставляется, и соответственно можно расчерчивать перспективы в пропорциональных размерах, например в золотом сечении, или логарифмическом. Т.е. по сути, менять константу преобразования миров, ведь ПИ только у нас 3.1415 и т.д. В сути это лишь коэффициент изгиба мира на шаг межмирья, как шаг витка пружины. Есть Пи и 2.8 и даже 1.6, соответственно фигура под наше ПИ=3.1415 имеет несколько иные размерности в мире с ПИ=2.8, и для этого пропорциональные расчёты весьма полезны. А мы всё циркуль, циркуль, а оно вона как - одним концом наши размеры, а другим концом размеры другого мира.
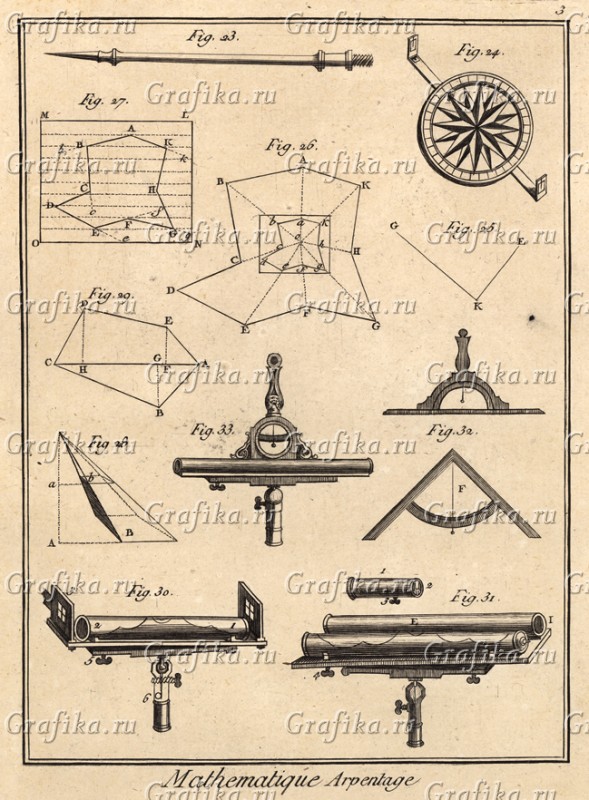
Mathematique Geometrie рис3: Всё та же работа с проекциями посредством визиров и даже щелевого визира. У геодезистов нынче нечто похожее, но без межмирных пропорциональных привязок. А если поглядеть на fig.26, то можно заметить, что размеченное на поверхности по линиям сил, что векторально едины для сонма миров, не обязательно параллельны и перпендикулярны, а иметь могут весьма витееватый контур. Мы ведь иногда удивляемся, что древние постройки, например, Замок или Кремль не чётко ровно построены, а имеют изгибающуюся конструкцию вроде бы прямых стен. Стены вроде прямые, а вот повороты на стыках башен у них не очень симметричны. Обращает внимание, что на плоскости отмечают не менее 7-и точек, где будут построены башни, между которыми будут протянуты прямые стены. При этом аналогичная конструкция иного мира, с иным ПИ, имеет пропорциональную структуру на своей местности, однако для наших линейных размеров она может быть иной. Проще говоря, в другом мире будет ну очень похожий Кремль или Замок. При этом они будут иметь не совсем симметричную конструкцию, искривлённую за счёт взаимного не совсем параллельного положения плоскостей миров. Именно поэтому, что кривизна разных миров разная, то и прямоугольник при нашем ПИ будет совсем иной фигурой в другом мире. Это как рисунок нарисованный на шарике, по мере его надувания или сдувания, может менять не только пропорции, но и геометрию.
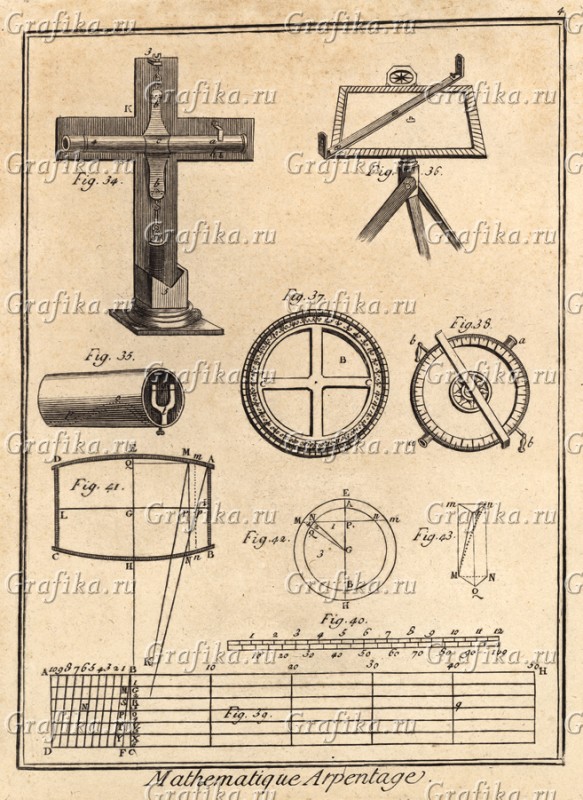
Mathematique Geometrie рис4: Визирные рейки позволяют привязывать карты к местности. На старых картах ещё по углам есть такие наклонные насечки, по которым их размечают для местности или проводят разворот схемы на местности. Визирные рамки fig.35, что мы бы назвали мушками для прицеливания, служили примерно той же цели, но как визиры для наведения, но отнюдь не стрельбы, а для определения перспектив и смещения, в биноклях на стёклах и нынче есть дальномерные риски. fig.34 чем-то напоминает крест? Трубой целимся? А если приладить градусный круг для измерения угла наклона fig.37? То… Ну что вы, кельтский крест? Разве такое может быть?
Optique рис10:
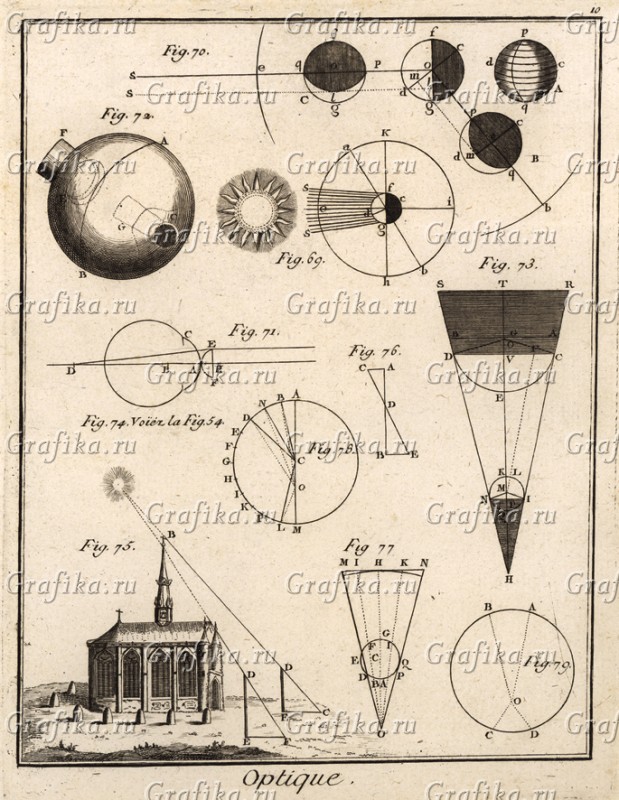
Fig69 - Так мы себе представляем мир Земли - Солнце светит, Земля освещена.
Fig70 - Так выглядит подлунный мир, где видимая нам тень проползает по объекты Луна. Но что это за загадочный объект, да ещё в полоску? Ведь он для нас с теменной стороны и фактически невидим! Но он есть! И естественно имеет значение.
Fig71 - Так преобразует видимый нам мир наш глаз, естественно внося искажения, которые мы вроде как не замечаем, ибо привыкли их автоматически компенсировать.
Fig72 - Так наблюдатель может нивелировать оптические искажения для наблюдения за миром, в обиходе это называют обсерваториями. Хотя мы их нацеливаем на звёзды, но они имеют более широкое применение.
Fig73 - Так выглядит видимый нам мир в искажении расширяющихся перспектив, где есть тёмные зоны для видимой нам оптики, т.е. имеются тени.
Fig75 - А тут мы видим простое и будничное измерение положения вовсе не Ярило Солнца, но измерение объекта при помощи банальных крестов с наклонной перекладиной! И абсолютно банальнейшим образом при помощи перспектив и таких простых визирных меток, обычным тригонометрическим образом рассчитывается высота завесы по этому объекту. А вот эти «солнечные часы» «D-Е-F» можно найти во дворах очень многих Фиортов, Церковен и даже Костёлов. А народ-то всё ломает голову, зачем на каменной площади посреди двора расчерчены всяческие «солнечные часы»? Ну, естественно чтобы время узнавать, а то, как же. И понятно же всем, что обсерваторий понастроили, чтобы знать, когда солнцестояние. И кресты ориентируют строго на Восток, чтобы значится смотреть на духовный центр и знать, куда лицо поворачивать, когда лбом об пол чечётку бить. А оно вона как, и палочка на кресте наклоняется строго по склонению объекта на нёбе, а не небе. И крест стоит тем боком, чтобы в полдень быть на линии объекта и чем выше установили крест, тем точнее измерение угловых размеров, через которые можно определить расстояние до завесы и видимого объекта. Но при этом, нетрудно заметить, что использованы на местности маркерами не башни, а банальные камни, которые отбрасывают тень! И такие камни вокруг культовых строений так же непонятны по назначению учёным в наше время! Т.е. объектом измерения служит вовсе не Солнце! А объект-то находится совсем с другой стороны!
Fig76, 77, 78, 79 - Банальная школьная тригонометрия. Считаем склонение, отклонение, вектор, поправки, перспективы и… И в пересечении пропорций, тех самых что расчерчивают по разным ПИ, мы ловим объект, что определяет нам… А тот самый проход через точку «С» как у Торнадо, который опускает свой хобот. Далее? А далее всё просто - есть местоположение прохода и делов-то. Собственно точно так же можно определить и дырку портала, что даёт и через которую проецирует нам тот или иной мираж реальный объект, что напрямую нам не видим, хотя который мы можем наблюдать хоть в пустыне, хоть на небе в преломлении через точку открывшегося портала. Это как через открытую дверь падает свет на дорогу, и мы видим тени и даже изображения. Но это лишь отражение объекта, что появился в проёме двери. И чтобы найти эту самую дверь, надо учитывать преломления векторов и брать поправки на перспективы и искривления миров.
В сути всё просто.
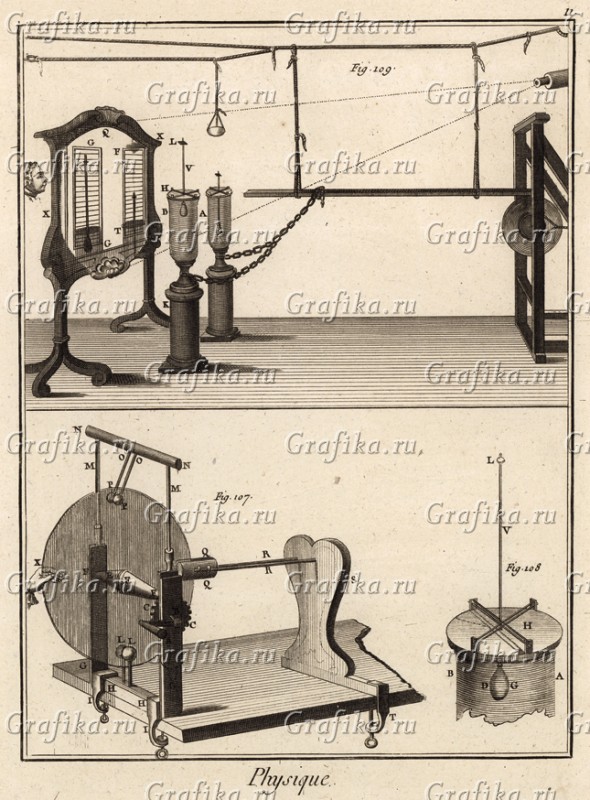
Physique стр11: Планка, мы бы сказали эбонитовая, весит на подвесе, причём уравновешенная. Зачем? Видимо надо соблюсти баланс? Но зачем цепочка идёт от банок? Видимо надо передать заряд? Заряд стекает на «палочку и она теряет баланс. Ведь «заряды» не растекаются на стержне, а скапливаются. Ну, кто изучал физику, про это знает. И значит «палочка» теряет равновесие! При этом справа подают пучок света, слева наблюдатель на экране видит уровни в стаканах. Уровни вроде одинаковы, но вот что за палочки плавают? А это ареометры. А зачем? Они показывают нам плотность жидкости в каждом стакане. И? И разность плотностей даёт нам заряд. Тот же принцип батарейки, но где жидкости не смешаны, как у нас в батарейке в одном флаконе и разъедают друг друга, перемешиваясь, сажая батарейку, а продолжая «вырабатывать» электричество. Батарейка ведь садится, как и аккумулятор не потому как куда-то утекает ток, а потому как разрушается их химическая структура. И вся мощь современной науки по улучшению батареек направлена на предотвращение химического разрушения материала батареек и аккумуляторов. И вот как только они придут к аналогичной схеме, батарейки будут практически вечными. Впрочем и тут плотность жидкостей меняется из-за воздействия внешней среды, а потому по этой причине можно измерять параметры внешней среды.
Ниже разрисована банальная элетрофорная машинка, позволяющая придавать динамический потенциал статического электричества другому концу палочки. И мы получаем отличный измеритель параметров среды дифференциального типа.
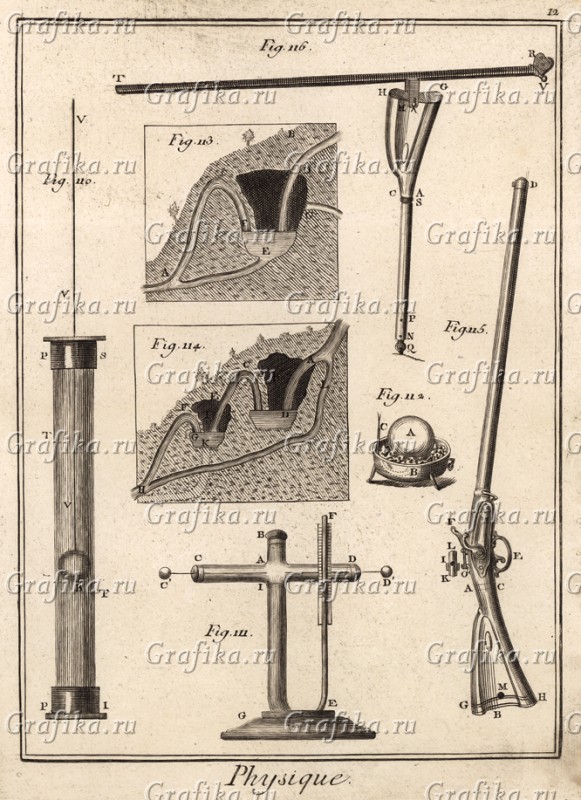
Physique стр12: Принцип работы с давлениями, в частности поднятие жидкости при помощи многоуровневых полостей. Духовое ружьё, уровни и даже уравновешенная на палочка, где при смене давления меняется угол наклона на оси, ввиду разности весов полости и груза.
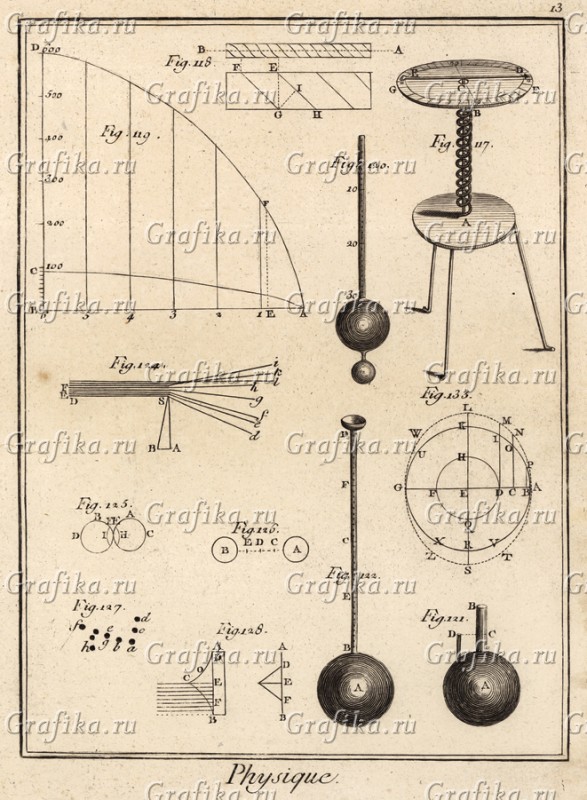
Physique стр13: Логарифмический измеритель, больше нам знакомый по банальному ртутному или спиртовому градуснику, где из-за расширения рабочей среды в цилиндре, мы получаем высоту столба по которому и судим об измеряемом параметре. Приборчик на табуретке со спиралью в практически таком же виде используется и нынче для измерения температур, ведь металлы расширяются и сжимаются при разных температурах и соответственно стрелка смещается. Если нить биметаллическая, то приор будет совсем маленький и используется в нашей современности в более компактном виде.

Physique стр17: Прибор весьма технологичен, ведь в колбе создаётся разряжение или давление, как бы мы сказали барокамера. Вон и ручка, которая тащит рейку, которая вытягивает поршень насоса, который выкачивает из колбы воздух на левом аппарате, потому колба присасывается внешним давлением. Или нагнетает давление, потому колба зажата в тисках. Как вариант это позволяет создавать на разности давлений потенциал между этими аппаратами, по сути как 2-е банки, которые вкупе дают заряд между собой. Обращает внимание шкала, которая проградуирована вовсе не в десятичной системе. И максимальное значение «3600». Те самые 36 градусов или 6х6. Сбоку идут знакомые 1-4-9-16-25-36-49… Знакомые «сакральные» числа. А откуда «0», ведь все числа не десятичные, а с параболическим нарастанием, ну логарифмическая шкала по-нашему. У нас ещё есть логарифмические линейки, которые сильно напоминают вычислители квадрантов, мы бы сказали ручные логарифмические арифмометры.
А «0» определяет эквипотенциальную поверхность, этакий круг, в пределах коего градиент среды единый и имеет схожие характеристики. Вот «360» - это 36 долей градиента. Мы ещё говорим градусы. А если счёт идёт в единицах «3600» т.е. по градиенту двух эквипотенциальных сред, то радианты. И тут мы считаем параметры среды между 2-х пределов. Собственно fig.167 рассчитывает по «360» (градусам) и используют логарифмическую линейку. А fig.168 - рассчитывая между 2-х полостей, там такая фигурка многогранная - это в «3600» (радиантах), фактически дифференцируем при этом по радиусным векторам. В этом случае требуется не логарифмическая линейка, а дифференцирующий квадрант. Т.е. та же тригонометрия, но применительно к реальному миру межмирных сред.
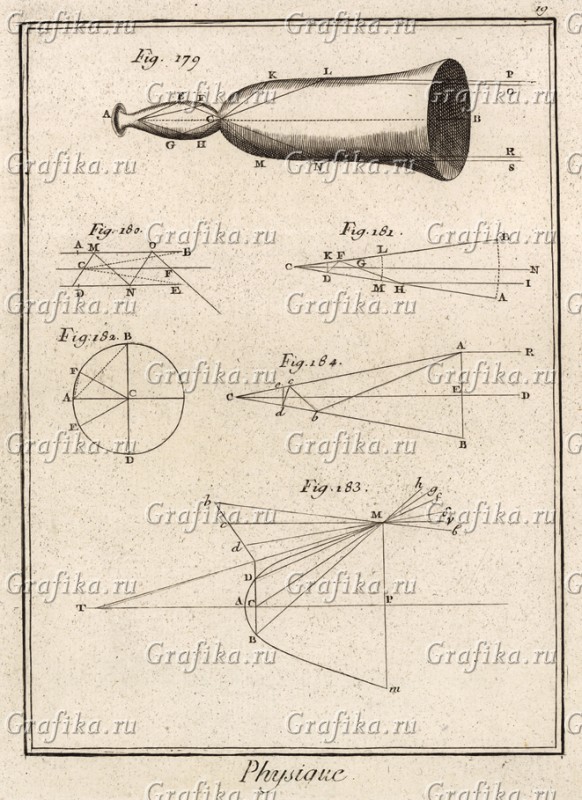
Physique стр19: Таких «ваз» по миру раскидано превеликое множество. Учёные даже посчитали, что они очень точно выверены на ту или иную звуковую частоту. Чистота ствола очень важна для поддержания настроек. Видна и точка излучения на расчётах. А ведь именно в этом месте располагаются странные дырочки, что заклёпаны и даже замазаны на разных древних вазах и трубах. А расчёты акустики и в нашем мире проходят точно так же.
Собственно для чего такое могло потребоваться помимо пугания друг друга громкими монотонными звуками. Например, задавать точную настройку среды, излучая в окружающее пространство определённый тон. Пространство подстраивается и… И даже может открыться межмирный переход, или изменятся параметры материи на которую настроен, скажем камень станет пластичным пока среда вокруг него сохраняет эти настройки. Мы ведь нагреваем воздух? И всё попавшее в это место меняет параметры под «нагрев», становясь немного иным, скажем, что-то делается пластичней, а что-то даже испаряется. Что-то преобразуется и прочее, прочее. «Нагрев» всего лишь изменение обертонов материи среды воздуха. Ну, ещё говорят, что молекулы начинают быстрее бегать и материя нагревается. А заставить «бегать» молекулы можно по-разному. Можно палкой по их заднице, можно голосом, подав команду. Ведь звук - это колебание среды? Значит попав в некоторые частоты, где среда начнёт синхронно реагировать, попав в резонанс, мы получаем изменение среды. Ну можно петь на одной ноте, или даже резонировать в некой мелодии, входя в раж.
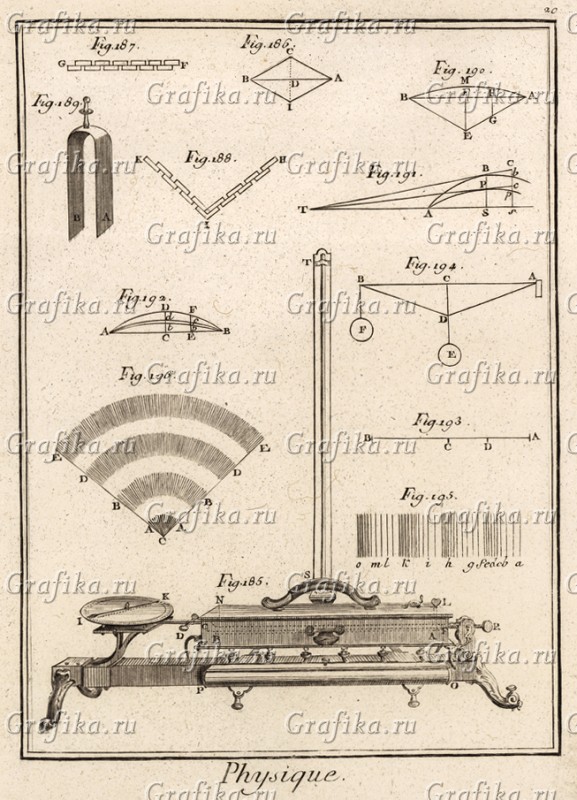
Physique стр20: Уже знакомые элементы собраны вместе. Вот нам и стрелка, что показывает отклонение уравновешенного стержня, как на обычных весах. И столбик логарифмического измерителя. Вот и графики нарастания. И даже интерференционные решётки, знакомы нем по поляризационным световым полосам, когда призма раскладывает свет. А тут разрисованы градиентные экстремумы fig.190, ну как расходящиеся круги на воде. И интерференционная частотная решётка fig.193. Вот аппарат fig.189 мы знаем как камертон, он по сути выполняет роль кварцевого резонатора, задающего эталонные параметры среды, под которые и производится замер. Ведь вот казалось бы, зачем на приборе странная трубка «P»-«О»? А она висит на подвесах, как та самая эбонитовая палочка и определяет частотные параметры среды. По сути измерение на преломлении сред.
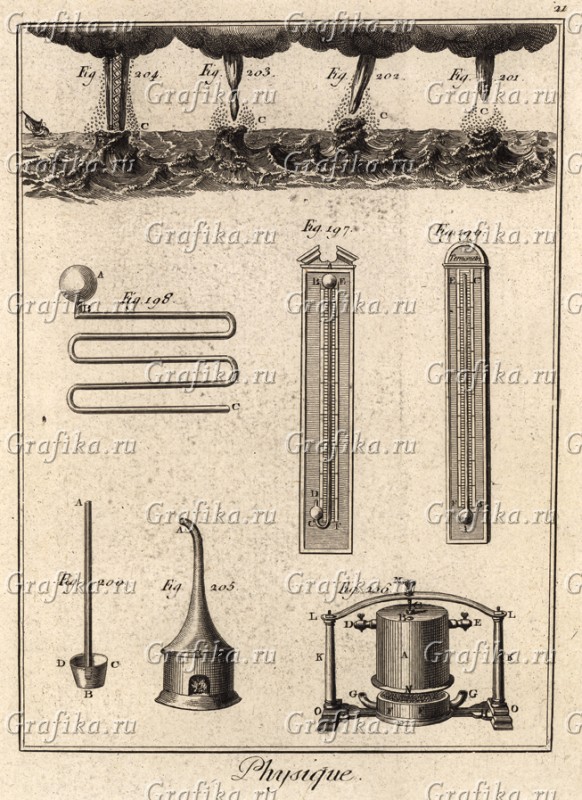
Physique стр21: Собственно барометр и термометр. Но зачем? А сверху видим несколько стадий Торнадо. Торнадо обыкновенное. Но в любом Торнадо необыкновенен глаз - это внутренняя среда, причём абсолютно отличная от внешней, которые разделены прослойкой вращающегося вихря. Торнадо устойчив, когда у него есть тональная ось, функционирующая в резонансе, по сути тот же портал, как открытый межмирный переход. Fig.204. И пока он устойчив, по этому каналу даже можно пройти. Однако Торнадо имеет буферную зону «С», которая по сути межмирная прослойка, типа ничейной земли, принадлежащая сразу 2-м мирам и никому конкретно. Именно эта зона «С» работает дверью, что соединяет связку порталов миров. А если посмотреть сводки, то можно заметить, что Торнадо не такое уж и редкое явление. А теперь, при помощи нагрева, «ведра» и барокамеры мы даже можем создать эту межмирную зону «С». Она вон там в ведре получается - хотите воду в вино перегоняйте, а хотите в коньяк или бензин.
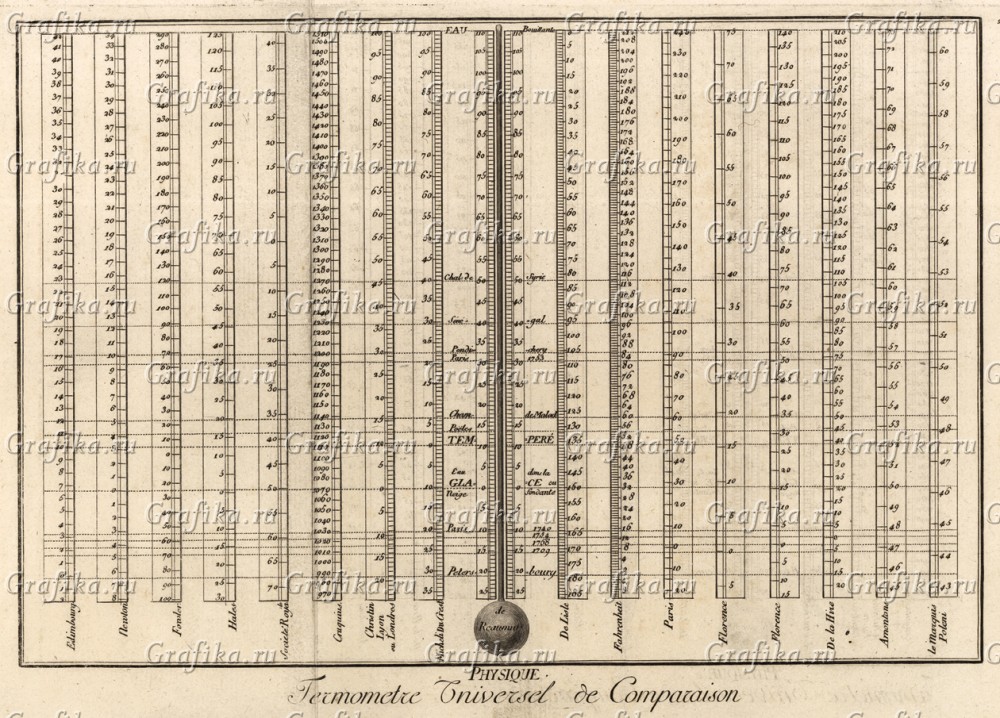
И естественно есть аля «Таблица Брадиса», что в табличном виде предоставляет нам цифры перевода параметров под разные линейные шкалы систем миров.
Все комментарии от Dmitrijan
Изображения взяты из источников указанных в посте: Александрийская библиотека. часть 2. http://pro-vladimir.livejournal.com/82962.html

Mathematique Geometrie рис1: Работа с пропорциями, как минимум 3 прибора, где fig.3 вроде как циркуль? Но что-то в нём смущает? А! Это пропорциональный циркуль! У него «гвоздик» переставляется, и соответственно можно расчерчивать перспективы в пропорциональных размерах, например в золотом сечении, или логарифмическом. Т.е. по сути, менять константу преобразования миров, ведь ПИ только у нас 3.1415 и т.д. В сути это лишь коэффициент изгиба мира на шаг межмирья, как шаг витка пружины. Есть Пи и 2.8 и даже 1.6, соответственно фигура под наше ПИ=3.1415 имеет несколько иные размерности в мире с ПИ=2.8, и для этого пропорциональные расчёты весьма полезны. А мы всё циркуль, циркуль, а оно вона как - одним концом наши размеры, а другим концом размеры другого мира.

Mathematique Geometrie рис3: Всё та же работа с проекциями посредством визиров и даже щелевого визира. У геодезистов нынче нечто похожее, но без межмирных пропорциональных привязок. А если поглядеть на fig.26, то можно заметить, что размеченное на поверхности по линиям сил, что векторально едины для сонма миров, не обязательно параллельны и перпендикулярны, а иметь могут весьма витееватый контур. Мы ведь иногда удивляемся, что древние постройки, например, Замок или Кремль не чётко ровно построены, а имеют изгибающуюся конструкцию вроде бы прямых стен. Стены вроде прямые, а вот повороты на стыках башен у них не очень симметричны. Обращает внимание, что на плоскости отмечают не менее 7-и точек, где будут построены башни, между которыми будут протянуты прямые стены. При этом аналогичная конструкция иного мира, с иным ПИ, имеет пропорциональную структуру на своей местности, однако для наших линейных размеров она может быть иной. Проще говоря, в другом мире будет ну очень похожий Кремль или Замок. При этом они будут иметь не совсем симметричную конструкцию, искривлённую за счёт взаимного не совсем параллельного положения плоскостей миров. Именно поэтому, что кривизна разных миров разная, то и прямоугольник при нашем ПИ будет совсем иной фигурой в другом мире. Это как рисунок нарисованный на шарике, по мере его надувания или сдувания, может менять не только пропорции, но и геометрию.

Mathematique Geometrie рис4: Визирные рейки позволяют привязывать карты к местности. На старых картах ещё по углам есть такие наклонные насечки, по которым их размечают для местности или проводят разворот схемы на местности. Визирные рамки fig.35, что мы бы назвали мушками для прицеливания, служили примерно той же цели, но как визиры для наведения, но отнюдь не стрельбы, а для определения перспектив и смещения, в биноклях на стёклах и нынче есть дальномерные риски. fig.34 чем-то напоминает крест? Трубой целимся? А если приладить градусный круг для измерения угла наклона fig.37? То… Ну что вы, кельтский крест? Разве такое может быть?

Optique рис10:
Fig69 - Так мы себе представляем мир Земли - Солнце светит, Земля освещена.
Fig70 - Так выглядит подлунный мир, где видимая нам тень проползает по объекты Луна. Но что это за загадочный объект, да ещё в полоску? Ведь он для нас с теменной стороны и фактически невидим! Но он есть! И естественно имеет значение.
Fig71 - Так преобразует видимый нам мир наш глаз, естественно внося искажения, которые мы вроде как не замечаем, ибо привыкли их автоматически компенсировать.
Fig72 - Так наблюдатель может нивелировать оптические искажения для наблюдения за миром, в обиходе это называют обсерваториями. Хотя мы их нацеливаем на звёзды, но они имеют более широкое применение.
Fig73 - Так выглядит видимый нам мир в искажении расширяющихся перспектив, где есть тёмные зоны для видимой нам оптики, т.е. имеются тени.
Fig75 - А тут мы видим простое и будничное измерение положения вовсе не Ярило Солнца, но измерение объекта при помощи банальных крестов с наклонной перекладиной! И абсолютно банальнейшим образом при помощи перспектив и таких простых визирных меток, обычным тригонометрическим образом рассчитывается высота завесы по этому объекту. А вот эти «солнечные часы» «D-Е-F» можно найти во дворах очень многих Фиортов, Церковен и даже Костёлов. А народ-то всё ломает голову, зачем на каменной площади посреди двора расчерчены всяческие «солнечные часы»? Ну, естественно чтобы время узнавать, а то, как же. И понятно же всем, что обсерваторий понастроили, чтобы знать, когда солнцестояние. И кресты ориентируют строго на Восток, чтобы значится смотреть на духовный центр и знать, куда лицо поворачивать, когда лбом об пол чечётку бить. А оно вона как, и палочка на кресте наклоняется строго по склонению объекта на нёбе, а не небе. И крест стоит тем боком, чтобы в полдень быть на линии объекта и чем выше установили крест, тем точнее измерение угловых размеров, через которые можно определить расстояние до завесы и видимого объекта. Но при этом, нетрудно заметить, что использованы на местности маркерами не башни, а банальные камни, которые отбрасывают тень! И такие камни вокруг культовых строений так же непонятны по назначению учёным в наше время! Т.е. объектом измерения служит вовсе не Солнце! А объект-то находится совсем с другой стороны!
Fig76, 77, 78, 79 - Банальная школьная тригонометрия. Считаем склонение, отклонение, вектор, поправки, перспективы и… И в пересечении пропорций, тех самых что расчерчивают по разным ПИ, мы ловим объект, что определяет нам… А тот самый проход через точку «С» как у Торнадо, который опускает свой хобот. Далее? А далее всё просто - есть местоположение прохода и делов-то. Собственно точно так же можно определить и дырку портала, что даёт и через которую проецирует нам тот или иной мираж реальный объект, что напрямую нам не видим, хотя который мы можем наблюдать хоть в пустыне, хоть на небе в преломлении через точку открывшегося портала. Это как через открытую дверь падает свет на дорогу, и мы видим тени и даже изображения. Но это лишь отражение объекта, что появился в проёме двери. И чтобы найти эту самую дверь, надо учитывать преломления векторов и брать поправки на перспективы и искривления миров.
В сути всё просто.

Physique стр11: Планка, мы бы сказали эбонитовая, весит на подвесе, причём уравновешенная. Зачем? Видимо надо соблюсти баланс? Но зачем цепочка идёт от банок? Видимо надо передать заряд? Заряд стекает на «палочку и она теряет баланс. Ведь «заряды» не растекаются на стержне, а скапливаются. Ну, кто изучал физику, про это знает. И значит «палочка» теряет равновесие! При этом справа подают пучок света, слева наблюдатель на экране видит уровни в стаканах. Уровни вроде одинаковы, но вот что за палочки плавают? А это ареометры. А зачем? Они показывают нам плотность жидкости в каждом стакане. И? И разность плотностей даёт нам заряд. Тот же принцип батарейки, но где жидкости не смешаны, как у нас в батарейке в одном флаконе и разъедают друг друга, перемешиваясь, сажая батарейку, а продолжая «вырабатывать» электричество. Батарейка ведь садится, как и аккумулятор не потому как куда-то утекает ток, а потому как разрушается их химическая структура. И вся мощь современной науки по улучшению батареек направлена на предотвращение химического разрушения материала батареек и аккумуляторов. И вот как только они придут к аналогичной схеме, батарейки будут практически вечными. Впрочем и тут плотность жидкостей меняется из-за воздействия внешней среды, а потому по этой причине можно измерять параметры внешней среды.
Ниже разрисована банальная элетрофорная машинка, позволяющая придавать динамический потенциал статического электричества другому концу палочки. И мы получаем отличный измеритель параметров среды дифференциального типа.

Physique стр12: Принцип работы с давлениями, в частности поднятие жидкости при помощи многоуровневых полостей. Духовое ружьё, уровни и даже уравновешенная на палочка, где при смене давления меняется угол наклона на оси, ввиду разности весов полости и груза.

Physique стр13: Логарифмический измеритель, больше нам знакомый по банальному ртутному или спиртовому градуснику, где из-за расширения рабочей среды в цилиндре, мы получаем высоту столба по которому и судим об измеряемом параметре. Приборчик на табуретке со спиралью в практически таком же виде используется и нынче для измерения температур, ведь металлы расширяются и сжимаются при разных температурах и соответственно стрелка смещается. Если нить биметаллическая, то приор будет совсем маленький и используется в нашей современности в более компактном виде.

Physique стр17: Прибор весьма технологичен, ведь в колбе создаётся разряжение или давление, как бы мы сказали барокамера. Вон и ручка, которая тащит рейку, которая вытягивает поршень насоса, который выкачивает из колбы воздух на левом аппарате, потому колба присасывается внешним давлением. Или нагнетает давление, потому колба зажата в тисках. Как вариант это позволяет создавать на разности давлений потенциал между этими аппаратами, по сути как 2-е банки, которые вкупе дают заряд между собой. Обращает внимание шкала, которая проградуирована вовсе не в десятичной системе. И максимальное значение «3600». Те самые 36 градусов или 6х6. Сбоку идут знакомые 1-4-9-16-25-36-49… Знакомые «сакральные» числа. А откуда «0», ведь все числа не десятичные, а с параболическим нарастанием, ну логарифмическая шкала по-нашему. У нас ещё есть логарифмические линейки, которые сильно напоминают вычислители квадрантов, мы бы сказали ручные логарифмические арифмометры.
А «0» определяет эквипотенциальную поверхность, этакий круг, в пределах коего градиент среды единый и имеет схожие характеристики. Вот «360» - это 36 долей градиента. Мы ещё говорим градусы. А если счёт идёт в единицах «3600» т.е. по градиенту двух эквипотенциальных сред, то радианты. И тут мы считаем параметры среды между 2-х пределов. Собственно fig.167 рассчитывает по «360» (градусам) и используют логарифмическую линейку. А fig.168 - рассчитывая между 2-х полостей, там такая фигурка многогранная - это в «3600» (радиантах), фактически дифференцируем при этом по радиусным векторам. В этом случае требуется не логарифмическая линейка, а дифференцирующий квадрант. Т.е. та же тригонометрия, но применительно к реальному миру межмирных сред.

Physique стр19: Таких «ваз» по миру раскидано превеликое множество. Учёные даже посчитали, что они очень точно выверены на ту или иную звуковую частоту. Чистота ствола очень важна для поддержания настроек. Видна и точка излучения на расчётах. А ведь именно в этом месте располагаются странные дырочки, что заклёпаны и даже замазаны на разных древних вазах и трубах. А расчёты акустики и в нашем мире проходят точно так же.
Собственно для чего такое могло потребоваться помимо пугания друг друга громкими монотонными звуками. Например, задавать точную настройку среды, излучая в окружающее пространство определённый тон. Пространство подстраивается и… И даже может открыться межмирный переход, или изменятся параметры материи на которую настроен, скажем камень станет пластичным пока среда вокруг него сохраняет эти настройки. Мы ведь нагреваем воздух? И всё попавшее в это место меняет параметры под «нагрев», становясь немного иным, скажем, что-то делается пластичней, а что-то даже испаряется. Что-то преобразуется и прочее, прочее. «Нагрев» всего лишь изменение обертонов материи среды воздуха. Ну, ещё говорят, что молекулы начинают быстрее бегать и материя нагревается. А заставить «бегать» молекулы можно по-разному. Можно палкой по их заднице, можно голосом, подав команду. Ведь звук - это колебание среды? Значит попав в некоторые частоты, где среда начнёт синхронно реагировать, попав в резонанс, мы получаем изменение среды. Ну можно петь на одной ноте, или даже резонировать в некой мелодии, входя в раж.

Physique стр20: Уже знакомые элементы собраны вместе. Вот нам и стрелка, что показывает отклонение уравновешенного стержня, как на обычных весах. И столбик логарифмического измерителя. Вот и графики нарастания. И даже интерференционные решётки, знакомы нем по поляризационным световым полосам, когда призма раскладывает свет. А тут разрисованы градиентные экстремумы fig.190, ну как расходящиеся круги на воде. И интерференционная частотная решётка fig.193. Вот аппарат fig.189 мы знаем как камертон, он по сути выполняет роль кварцевого резонатора, задающего эталонные параметры среды, под которые и производится замер. Ведь вот казалось бы, зачем на приборе странная трубка «P»-«О»? А она висит на подвесах, как та самая эбонитовая палочка и определяет частотные параметры среды. По сути измерение на преломлении сред.

Physique стр21: Собственно барометр и термометр. Но зачем? А сверху видим несколько стадий Торнадо. Торнадо обыкновенное. Но в любом Торнадо необыкновенен глаз - это внутренняя среда, причём абсолютно отличная от внешней, которые разделены прослойкой вращающегося вихря. Торнадо устойчив, когда у него есть тональная ось, функционирующая в резонансе, по сути тот же портал, как открытый межмирный переход. Fig.204. И пока он устойчив, по этому каналу даже можно пройти. Однако Торнадо имеет буферную зону «С», которая по сути межмирная прослойка, типа ничейной земли, принадлежащая сразу 2-м мирам и никому конкретно. Именно эта зона «С» работает дверью, что соединяет связку порталов миров. А если посмотреть сводки, то можно заметить, что Торнадо не такое уж и редкое явление. А теперь, при помощи нагрева, «ведра» и барокамеры мы даже можем создать эту межмирную зону «С». Она вон там в ведре получается - хотите воду в вино перегоняйте, а хотите в коньяк или бензин.

И естественно есть аля «Таблица Брадиса», что в табличном виде предоставляет нам цифры перевода параметров под разные линейные шкалы систем миров.
Все комментарии от Dmitrijan
Изображения взяты из источников указанных в посте: Александрийская библиотека. часть 2. http://pro-vladimir.livejournal.com/82962.html