Тождество для косинусов Pi/19 с кубическими корнями.
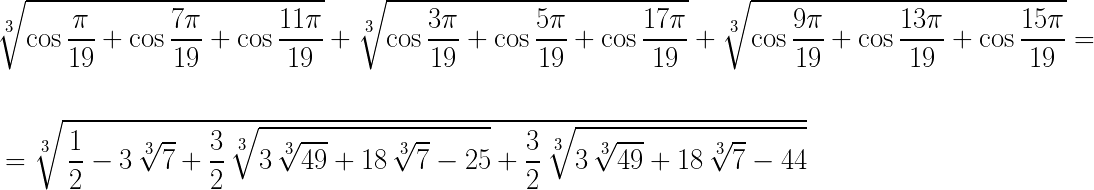
Проверка в Maple с точностью до 1000 знаков и код для желающих вставить в какую-нибудь другую программу:

Digits:=1000;
left:=surd(cos(3*Pi/19)+cos(5*Pi/19)+cos(17*Pi/19),3)+surd(cos(Pi/19)+cos(7*Pi/19)+cos(11*Pi/19),3)+surd(cos(9*Pi/19)+cos(13*Pi/19)+cos(15*Pi/19),3);
right:=(1/2-3*7^(1/3)+3/2*(-25+3*7^(2/3)+18*7^(1/3))^(1/3)+3/2*(-44+18*7^(1/3)+3*7^(2/3))^(1/3))^(1/3);
evalf(left-right);
Это число (левая и правая часть тождества) является корнем уравнения
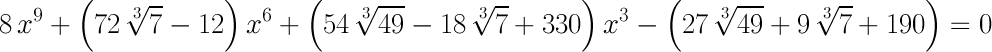
8*x^9+(72*7^(1/3)-12)*x^6+(54*49^(1/3)-18*7^(1/3)+330)*x^3-(27*49^(1/3)+9*7^(1/3)+190)
Спасибо a_shen, dimpas, jedal, posic, relf за помощь.
Ну что, профессионалы теории Галуа - может Ваша теория объяснить, почему корень кубический из семи? Ладно бы из 19, а то из 7... И почему вообще выражение выражается через корни из действительных величин? Ведь сам по себе cos(Pi/19) нельзя выразить через корни только от действительных чисел...
Я действовал по методике, изложенной тут: http://kvant.mccme.ru/1988/06/tri_formuly_ramanudzhana.htm
UPD: выложил ещё на два форума:
http://dxdy.ru/topic54521.html
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=38&t=461077