Как читать точечные диаграммы, или О достоверности эконометрических гипотез
Не так давно я задал своим читателям вопрос, на который не получил ответа: На графике мы видим примерно (2009-1980)*4 = 116 точек, отражающих ситуацию по отдельным кварталам (данные по ВВП, а значит и его изменению, рассчитываются в США поквартально). Так вот, насколько достоверны - с точки зрения матстатистики - выводы, сделанные на основе такого количества измерений?. Раз читатели не знают, значит моя очередь; итак, смотрим на точечные диаграммы и учимся видеть.
Всякое обучение видению начинается с понимания того, что именно требуется увидеть. Так шахматист, бросивший один взгляд на позицию, дает комментарий - "Где были фигуры, не помню, но у черных явное преимущество". Шахматист видит на доске главное (соотношение сил), сторонний наблюдатель - всего лишь фигуры.
Что же мы собираемся увидеть на точечных диаграммах? Во-первых, связаны ли друг с другом показатели, отложенные по осям координат. Во-вторых - насколько можно быть уверенным в том, что они действительно между собой связаны, а не "просто совпало".
На первый вопрос точечные диаграммы отвечают идеально - по ним сразу видно, есть связь между параметрами или нет. А вот чтобы увидеть, насколько она достоверна, нужно немного потренировать глаз. В эконометрике надежность связи между двумя показателями определяется путем проверки "нулевой гипотезы". В линейном приближении Y = A + B*X + ошибка измерения; отсутствие всякой связи между Y и X означает, что B=0, а Y = A + ошибка. Появление на графике Y=f(X) сколько-нибудь выраженного тренда может означать либо наличие связи между Y и X, либо случайное возникновение тренда исключительно из-за ошибок измерения. Вероятность второго варианта тем меньше, чем круче тренд и чем меньше разброс точек вокруг него. Все, что нам нужно увидеть для успешного чтения диаграмм - картинки, соответствующие разным уровням вероятности "нулевой гипотезы".
Вот я и нарисовал в Экселе серию картинок, сгенерировав методом Монте-Карло несколько наборов значений Y = 5 + 0.5*X + ошибка, с разными уровнями ошибок. Смотрим на результат:
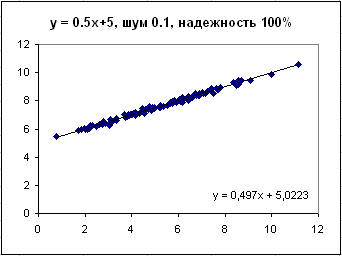
Здесь все понятно - показатели не просто связаны, а могут быть прям-таки рассчитаны один через другой. При матожидании Y в 7.5 среднеквадратичная ошибка здесь 0.1, чуть больше процента, и никак не влияет на результат.
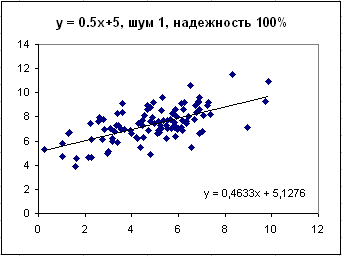
Ошибка составляет уже 1 единицу на 7.5 - около 15%, - однако связь двух показателей по-прежнему видна невооруженным глазом, а также 100% достоверна.
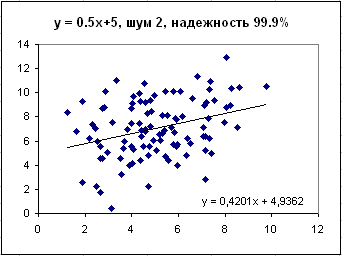
Увеличиваем ошибку до 2 единиц. Достоверность связи 99.9% (по статформулам), а вот на глаз она уже такой совсем не выглядит.
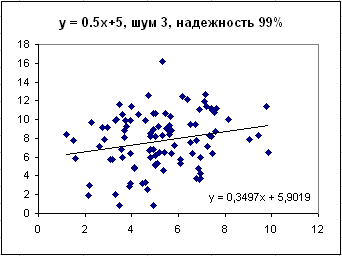
Достоверность связи 99%, а на глаз - совсем слабая зависимость.
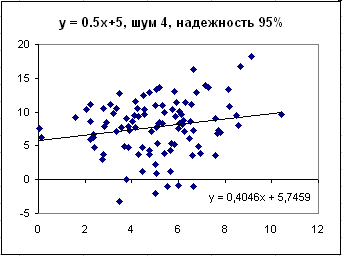
95% достоверность, визуально диаграмма почти не отличается от предыдущей.
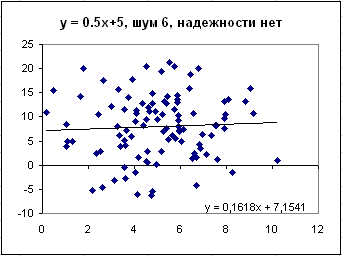
И наконец, только при ошибке, сопоставимой со средним значением показателя (6 и 7.5) появляется ситуация, в которой отбросить нулевую гипотезу уже не получается. На этой картинке мы наконец видим отсутствие значимой связи.
Честно говоря, построив диаграммы, я был удивлен, насколько достоверной оказывается связь двух показателей при громадных, на мой взгляд, разбросах значений. Поглядев теперь на заинтересовавший меня график "закона Окуня":

- я больше не буду задавать вопрос "насколько этому можно верить?". По приведенной выше методике, диаграмма демонстрирует 100% вероятность связи между изменениями ВВП и безработицей, и вполне заслуживает названия "закона".
Вот другой характерный пример (via kapterev). В статье AJ Oswald and S Wu ‘Objective Confirmation of Subjective Measures of Human Well-being: Evidence from the USA’, Science, online 17 December 2009 приводится такой вот график связи между номером штата в рейтинге по "объективному качеству жизни" и уровнем удовлетворенности этой жизнью у населения:
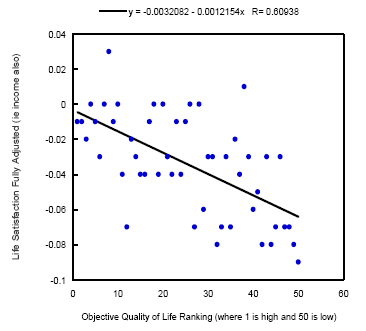
На первый взгляд, мешанина точек, из которой ничего не следует. А вот если пройти предварительную тренировку (см. выше) - наоборот, 99.9% достоверная связь между двумя показателями.
Итак, любая точечная диаграмма, на которой можно разглядеть хоть какой-нибудь тренд, с точки зрения эконометрики уже закон. Любая.
Что-то здесь не так, не правда ли? И верно, не так. Но об этом - в следующей серии.
Всякое обучение видению начинается с понимания того, что именно требуется увидеть. Так шахматист, бросивший один взгляд на позицию, дает комментарий - "Где были фигуры, не помню, но у черных явное преимущество". Шахматист видит на доске главное (соотношение сил), сторонний наблюдатель - всего лишь фигуры.
Что же мы собираемся увидеть на точечных диаграммах? Во-первых, связаны ли друг с другом показатели, отложенные по осям координат. Во-вторых - насколько можно быть уверенным в том, что они действительно между собой связаны, а не "просто совпало".
На первый вопрос точечные диаграммы отвечают идеально - по ним сразу видно, есть связь между параметрами или нет. А вот чтобы увидеть, насколько она достоверна, нужно немного потренировать глаз. В эконометрике надежность связи между двумя показателями определяется путем проверки "нулевой гипотезы". В линейном приближении Y = A + B*X + ошибка измерения; отсутствие всякой связи между Y и X означает, что B=0, а Y = A + ошибка. Появление на графике Y=f(X) сколько-нибудь выраженного тренда может означать либо наличие связи между Y и X, либо случайное возникновение тренда исключительно из-за ошибок измерения. Вероятность второго варианта тем меньше, чем круче тренд и чем меньше разброс точек вокруг него. Все, что нам нужно увидеть для успешного чтения диаграмм - картинки, соответствующие разным уровням вероятности "нулевой гипотезы".
Вот я и нарисовал в Экселе серию картинок, сгенерировав методом Монте-Карло несколько наборов значений Y = 5 + 0.5*X + ошибка, с разными уровнями ошибок. Смотрим на результат:

Здесь все понятно - показатели не просто связаны, а могут быть прям-таки рассчитаны один через другой. При матожидании Y в 7.5 среднеквадратичная ошибка здесь 0.1, чуть больше процента, и никак не влияет на результат.

Ошибка составляет уже 1 единицу на 7.5 - около 15%, - однако связь двух показателей по-прежнему видна невооруженным глазом, а также 100% достоверна.

Увеличиваем ошибку до 2 единиц. Достоверность связи 99.9% (по статформулам), а вот на глаз она уже такой совсем не выглядит.

Достоверность связи 99%, а на глаз - совсем слабая зависимость.

95% достоверность, визуально диаграмма почти не отличается от предыдущей.

И наконец, только при ошибке, сопоставимой со средним значением показателя (6 и 7.5) появляется ситуация, в которой отбросить нулевую гипотезу уже не получается. На этой картинке мы наконец видим отсутствие значимой связи.
Честно говоря, построив диаграммы, я был удивлен, насколько достоверной оказывается связь двух показателей при громадных, на мой взгляд, разбросах значений. Поглядев теперь на заинтересовавший меня график "закона Окуня":

- я больше не буду задавать вопрос "насколько этому можно верить?". По приведенной выше методике, диаграмма демонстрирует 100% вероятность связи между изменениями ВВП и безработицей, и вполне заслуживает названия "закона".
Вот другой характерный пример (via kapterev). В статье AJ Oswald and S Wu ‘Objective Confirmation of Subjective Measures of Human Well-being: Evidence from the USA’, Science, online 17 December 2009 приводится такой вот график связи между номером штата в рейтинге по "объективному качеству жизни" и уровнем удовлетворенности этой жизнью у населения:

На первый взгляд, мешанина точек, из которой ничего не следует. А вот если пройти предварительную тренировку (см. выше) - наоборот, 99.9% достоверная связь между двумя показателями.
Итак, любая точечная диаграмма, на которой можно разглядеть хоть какой-нибудь тренд, с точки зрения эконометрики уже закон. Любая.
Что-то здесь не так, не правда ли? И верно, не так. Но об этом - в следующей серии.