Порабощаем shootout, блинчеги
Продолжаем развлекаться =)
Итак, позорно слив жабе в предыдущей серии (так и не разобрался, как приклеивать треды к ядрам), я решил попробовать взять реванш в какой-нибудь другой задачке, которая была бы чуток более алгоритмической, нежели системной.
Выбор пал на fannkuch-redux, для которого (как и для хамелеонов) отсутствовала Lisp/SBCL-реализация. Итак,
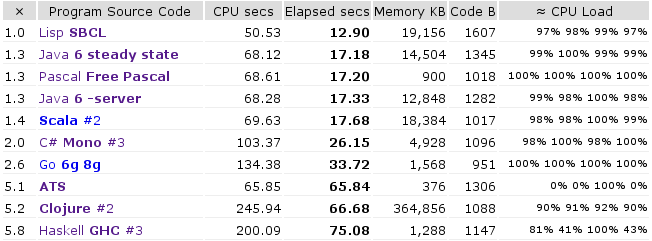
OWNED, причем без шансов. Как видно из картинки, предыдущие лидеры там толпятся как бараны вокруг отметки в 17 секунд. Пожалуй, что для стандартного подхода к решению это предел.
Я же решил зайти с основного козыря CL: сгенерить максимально специфический для входных данных код, а потом отважно его исполнить.
(defun main (&optional force-n)
(let* ((args (cdr sb-ext:*posix-argv*))
(n (or force-n (if args (parse-integer (car args)) 12))))
(multiple-value-bind (checksum max-flips-count)
(funcall (the function (eval `(deffannkuch ,n :workers 4 :worker-chunk-size 12000))))
(format t "~a~%Pfannkuchen(~a) = ~a~%" checksum n max-flips-count))))
Заметили там мигающий "eval"? =) Вот это оно. Между прочим, +0.35 секунд на кодогенерацию + компиляцию в рантайме.
Итак, теперь вкрадце о задаче. На вход подается число N, допустим, 4.
Этап первый: надо сгенерировать все перестановки 1 .. N чисел. Для четырех это 1234, 2134, 2314, 3214 и так далее (всего 24 перестановки - 4!). Вроде пока ок, но тут небольшая засада: последовательность генерации перестановок строго заданная (в разделе с описанием приведены данные и ссылка на алгоритм, как такую последовательность генерить).
Этап второй: берем очередную перестановку (допустим, 4132), берем первый элемент (4) и меняем порядок следования такого количества элементов в последовательности на обратный: 2314. Считаем, сколько раз надо произвести такую операцию, чтобы получить в начале единицу: 4132 -> 2314 -> 3214 -> 1234, итого 3 переворота.
Этап третий: считаем количество переворотов для каждой пермутации (хехе), запоминая максимальное их количество и высчитывая простенькую контрольную сумму, цель которой заключается в том, чтоб проследить, не накосячили ли мы с последовательностью перестановок.
В итоге нужно получить контрольную сумму и максимальное количество переворотов среди всех перестановок. Для N=4 максимальное количество переворотов равно четырем (последовательность "2413").
Наверно, самая наглядная реализация здесь -- это питонячья версия (решение в лоб). Всего 45 строк, но с более чем пятисоткратным отставанием по быстродействию от лидера (от меня, тоесть =)). Остальные решения пытаются применять всяческие оптимизации, и здесь наилучшего результата добился Oleg Mazurov со своей жаба-версией.
Я же решил действовать хитростью и коварством (ну как обычно). Мой стандартный алгоритм метапрограммирования выглядит так:
Итак, положим, у нас фиксированная N, например, 3. Как бы я написал максимально шуструю программу, печатающую все последовательности? Очевидно, вот так =)
(format t "123, 213, 231, 321, 312, 132, ")
Надо сказать, это решение отлично ложиться на целый класс задач. Понятное дело, что если что-то можно заранее вычислить на компиляции, то это надо вычислить на компиляции. Но для конкретного нашего задания такое низкое коварство не пройдет: напомню, что компиляция там все равно идет на рантайме (eval), да и предвычисление перестановок для 12 элементов даст 12! вариантов (почти полмиллиарда). Поэтому в любом случае нам придется генерировать циклы, разумеется, по-возможности, максимально их разворачивая. Вот как-то так:
(let ((tmp-0 1) (tmp-1 2) (tmp-2 3))
(loop :repeat 3
:do (prog1
(let ((tmp-3 tmp-0) (tmp-4 tmp-1))
(loop :repeat 2
:do (prog1
(let ((a tmp-3) (b tmp-4) (c tmp-2))
(format t "~a~a~a, " a b c)
(let ((first tmp-3))
(setf tmp-3 tmp-4
tmp-4 first)))))
(let ((first tmp-0))
(setf tmp-0 tmp-1
tmp-1 tmp-2
tmp-2 first))))))
На самом деле, стоит только прикинуть вид "максимально специфичной" для конкретных зафиксированных данных программы, как сразу становится ясен паттерн, как их генерировать. Я здесь выделил цветами RGB, соответственно, первый, второй и третий цикл в порядке их вложенности. В конце каждой итерации каждый цикл делает rotate для своих элементов, в соответствии с алгоритмом генерации перестановок. Для последнего (третьего) вложенного цикла объявление loop опущено (так как там получился бы бессмысленный ":repeat 1") и никакие элементы не сдвигаются (так как там только один, последний).
По-моему, паттерн ясен, понятен, нагляден и вообще всем хорош =) Соответственно, для перестановок N элементов мы генерим N вложенных циклов, причем каждый i-ый цикл объявляет себе (N - i) переменных, затеняя такие же родительские и наследуя остальные. Свои переменные он в конце итерации ротирует, родительские не трогает. Суммарно, например, для N=12 будет объявленно (12+11+10+9+8+7+6+5+4+3+2+12)=89 переменных.
Для пермутаций у нас уже практически все готово, осталось дополнить генерирующийся код дополнительными проверками на останов для частичной генерации перестановок - это пригодится для разбрасывания работы по процессорам. Вот конечный макрос:
FANNKUCH-REDUX> (let ((start-from 0) (total-count 24))
(with-permutations ((a b c d) start-from total-count)
(format t "~a~a~a~a, " a b c d)))
0123, 1023, 1203, 2103, 2013, 0213, 1230, 2130, 2310, 3210, 3120, 1320, 2301, ...
Реализацию можно посмотреть в коде бенчмарка, она небольшая: исходник.
Далее, что касается подсчета количества переворотов (flips). Здесь все еще элементарней: зная N, легко сгенерировать необходимый switch/case:
FANNKUCH-REDUX> (macroexpand
'(with-flips-count ((a b c d) flips-count)
'my-code-here))
(LET ((FLIPS-COUNT 0))
(DECLARE (TYPE FIXNUM FLIPS-COUNT))
(UNLESS (ZEROP A)
(LOOP (INCF FLIPS-COUNT)
(COND ((= A 1) (WHEN (ZEROP B) (RETURN)) (ROTATEF A B))
((= A 2) (WHEN (ZEROP C) (RETURN)) (ROTATEF A C))
((= A 3) (WHEN (ZEROP D) (RETURN)) (ROTATEF A D) (ROTATEF B C)))))
'MY-CODE-HERE)
T
Ну и все, теперь у нас в зубах достаточно инструментов, чтобы легко и припеваючи решить всю задачу для фиксированного N. Вот так, например, это будет для N=5 (я для наглядности подсветил вышеприведенные макросы):
(let ((max-flips-count 0)
(checksum 0)
(sign t)
(start-from 0)
(total-count 120))
(with-permutations ((a b c d e) start-from total-count)
(with-flips-count ((a b c d e) flips-count)
(when (> flips-count max-flips-count)
(setf max-flips-count flips-count))
(incf checksum (if sign flips-count (- flips-count)))
(setf sign (not sign))))
(values checksum max-flips-count))
Ну а теперь дело техники. Раскидать работу поблочно на процессоры и собрать обратно контрольную сумму и максимальное количество переворотов от воркеров. И далее все как я приводил в начале статьи: берем из аргументов командной строки заданную N и в рантайме производим кодогенерацию программы, которую затем и выполняем.
Вот собственно и все. Надеюсь, мне удалось доступно объяснить подход с кодогенерацией максимально специфичного кода для решения сложных вычислительных задач. А позиция в рейтинге должна служить пруфом его эффективности =)
Итак, позорно слив жабе в предыдущей серии (так и не разобрался, как приклеивать треды к ядрам), я решил попробовать взять реванш в какой-нибудь другой задачке, которая была бы чуток более алгоритмической, нежели системной.
Выбор пал на fannkuch-redux, для которого (как и для хамелеонов) отсутствовала Lisp/SBCL-реализация. Итак,

OWNED, причем без шансов. Как видно из картинки, предыдущие лидеры там толпятся как бараны вокруг отметки в 17 секунд. Пожалуй, что для стандартного подхода к решению это предел.
Я же решил зайти с основного козыря CL: сгенерить максимально специфический для входных данных код, а потом отважно его исполнить.
(defun main (&optional force-n)
(let* ((args (cdr sb-ext:*posix-argv*))
(n (or force-n (if args (parse-integer (car args)) 12))))
(multiple-value-bind (checksum max-flips-count)
(funcall (the function (eval `(deffannkuch ,n :workers 4 :worker-chunk-size 12000))))
(format t "~a~%Pfannkuchen(~a) = ~a~%" checksum n max-flips-count))))
Заметили там мигающий "eval"? =) Вот это оно. Между прочим, +0.35 секунд на кодогенерацию + компиляцию в рантайме.
Итак, теперь вкрадце о задаче. На вход подается число N, допустим, 4.
Этап первый: надо сгенерировать все перестановки 1 .. N чисел. Для четырех это 1234, 2134, 2314, 3214 и так далее (всего 24 перестановки - 4!). Вроде пока ок, но тут небольшая засада: последовательность генерации перестановок строго заданная (в разделе с описанием приведены данные и ссылка на алгоритм, как такую последовательность генерить).
Этап второй: берем очередную перестановку (допустим, 4132), берем первый элемент (4) и меняем порядок следования такого количества элементов в последовательности на обратный: 2314. Считаем, сколько раз надо произвести такую операцию, чтобы получить в начале единицу: 4132 -> 2314 -> 3214 -> 1234, итого 3 переворота.
Этап третий: считаем количество переворотов для каждой пермутации (хехе), запоминая максимальное их количество и высчитывая простенькую контрольную сумму, цель которой заключается в том, чтоб проследить, не накосячили ли мы с последовательностью перестановок.
В итоге нужно получить контрольную сумму и максимальное количество переворотов среди всех перестановок. Для N=4 максимальное количество переворотов равно четырем (последовательность "2413").
Наверно, самая наглядная реализация здесь -- это питонячья версия (решение в лоб). Всего 45 строк, но с более чем пятисоткратным отставанием по быстродействию от лидера (от меня, тоесть =)). Остальные решения пытаются применять всяческие оптимизации, и здесь наилучшего результата добился Oleg Mazurov со своей жаба-версией.
Я же решил действовать хитростью и коварством (ну как обычно). Мой стандартный алгоритм метапрограммирования выглядит так:
- Представить себе, как должна выглядеть максимально производительная программа, при условии фиксированных входных данных (все константы).
- Написать программу, которая по заданным входным данным генерирует такую "максимально производительную программу".
Итак, положим, у нас фиксированная N, например, 3. Как бы я написал максимально шуструю программу, печатающую все последовательности? Очевидно, вот так =)
(format t "123, 213, 231, 321, 312, 132, ")
Надо сказать, это решение отлично ложиться на целый класс задач. Понятное дело, что если что-то можно заранее вычислить на компиляции, то это надо вычислить на компиляции. Но для конкретного нашего задания такое низкое коварство не пройдет: напомню, что компиляция там все равно идет на рантайме (eval), да и предвычисление перестановок для 12 элементов даст 12! вариантов (почти полмиллиарда). Поэтому в любом случае нам придется генерировать циклы, разумеется, по-возможности, максимально их разворачивая. Вот как-то так:
(let ((tmp-0 1) (tmp-1 2) (tmp-2 3))
(loop :repeat 3
:do (prog1
(let ((tmp-3 tmp-0) (tmp-4 tmp-1))
(loop :repeat 2
:do (prog1
(let ((a tmp-3) (b tmp-4) (c tmp-2))
(format t "~a~a~a, " a b c)
(let ((first tmp-3))
(setf tmp-3 tmp-4
tmp-4 first)))))
(let ((first tmp-0))
(setf tmp-0 tmp-1
tmp-1 tmp-2
tmp-2 first))))))
На самом деле, стоит только прикинуть вид "максимально специфичной" для конкретных зафиксированных данных программы, как сразу становится ясен паттерн, как их генерировать. Я здесь выделил цветами RGB, соответственно, первый, второй и третий цикл в порядке их вложенности. В конце каждой итерации каждый цикл делает rotate для своих элементов, в соответствии с алгоритмом генерации перестановок. Для последнего (третьего) вложенного цикла объявление loop опущено (так как там получился бы бессмысленный ":repeat 1") и никакие элементы не сдвигаются (так как там только один, последний).
По-моему, паттерн ясен, понятен, нагляден и вообще всем хорош =) Соответственно, для перестановок N элементов мы генерим N вложенных циклов, причем каждый i-ый цикл объявляет себе (N - i) переменных, затеняя такие же родительские и наследуя остальные. Свои переменные он в конце итерации ротирует, родительские не трогает. Суммарно, например, для N=12 будет объявленно (12+11+10+9+8+7+6+5+4+3+2+12)=89 переменных.
Для пермутаций у нас уже практически все готово, осталось дополнить генерирующийся код дополнительными проверками на останов для частичной генерации перестановок - это пригодится для разбрасывания работы по процессорам. Вот конечный макрос:
FANNKUCH-REDUX> (let ((start-from 0) (total-count 24))
(with-permutations ((a b c d) start-from total-count)
(format t "~a~a~a~a, " a b c d)))
0123, 1023, 1203, 2103, 2013, 0213, 1230, 2130, 2310, 3210, 3120, 1320, 2301, ...
Реализацию можно посмотреть в коде бенчмарка, она небольшая: исходник.
Далее, что касается подсчета количества переворотов (flips). Здесь все еще элементарней: зная N, легко сгенерировать необходимый switch/case:
FANNKUCH-REDUX> (macroexpand
'(with-flips-count ((a b c d) flips-count)
'my-code-here))
(LET ((FLIPS-COUNT 0))
(DECLARE (TYPE FIXNUM FLIPS-COUNT))
(UNLESS (ZEROP A)
(LOOP (INCF FLIPS-COUNT)
(COND ((= A 1) (WHEN (ZEROP B) (RETURN)) (ROTATEF A B))
((= A 2) (WHEN (ZEROP C) (RETURN)) (ROTATEF A C))
((= A 3) (WHEN (ZEROP D) (RETURN)) (ROTATEF A D) (ROTATEF B C)))))
'MY-CODE-HERE)
T
Ну и все, теперь у нас в зубах достаточно инструментов, чтобы легко и припеваючи решить всю задачу для фиксированного N. Вот так, например, это будет для N=5 (я для наглядности подсветил вышеприведенные макросы):
(let ((max-flips-count 0)
(checksum 0)
(sign t)
(start-from 0)
(total-count 120))
(with-permutations ((a b c d e) start-from total-count)
(with-flips-count ((a b c d e) flips-count)
(when (> flips-count max-flips-count)
(setf max-flips-count flips-count))
(incf checksum (if sign flips-count (- flips-count)))
(setf sign (not sign))))
(values checksum max-flips-count))
Ну а теперь дело техники. Раскидать работу поблочно на процессоры и собрать обратно контрольную сумму и максимальное количество переворотов от воркеров. И далее все как я приводил в начале статьи: берем из аргументов командной строки заданную N и в рантайме производим кодогенерацию программы, которую затем и выполняем.
Вот собственно и все. Надеюсь, мне удалось доступно объяснить подход с кодогенерацией максимально специфичного кода для решения сложных вычислительных задач. А позиция в рейтинге должна служить пруфом его эффективности =)