Видно ли Солнце с Проксимы Центавра? (часть II)
Первая часть
С яркостью мы разобрались, с освещённостью, вроде, тоже, теперь мы должны разобраться в том, что же такое реальная яркость, как её можно измерить? А измерить нам надо истинный блеск (intrinsic brightness), и чтобы найти истинный, надо учесть все факторы, снижающие яркость звёзд... Как мы знаем, в космосе есть не только вакуум (шутка), но и звёзды, планеты, а ещё и пыль, именно космическая пыль снижает яркость звёзд (это явление называется "межзвёздная экстинкция", от слова exstinctio - гашение). Ещё есть межзвёздный газ, который также влияет на яркость, точнее, на пропускание фотонов от звезды к наблюдателю на Земле, если мы устраним все эти препятствия, то получим реальную или истинную яркость звезды.
Чтобы понимать масштабы этого явления, вспомним, что мы уже знаем о звёздных величинах, конечно же, экстинция уменьшает звёздную величину объекта на 1,8m за килопарсек (примерно 3000 световых лет, вспомним размеры нашего Млечного Пути, которые составляют 100 000 световых лет в поперечнике и получим, что звёзды на другой стороне Млечного Пути мы просто не увидим, т.к. уменьшение звёздной величины будет около 50m, т.к. падение яркости произойдёт в 2,512^50 = 1*10^170 раз, что невероятно много!). Теперь, чтобы как-то соотнести реальные яркости звёзд между собой, их надо удалить на одно и то же расстояние (мысленно, конечно, мы же не боги) от Земли, тогда получим истинный блеск звёзд или абсолютную звёздную величину, т.к. освещённость не будет зависеть от расстояния, а только от самой звёзды, массы и температуры её поверхности. Удалить надо на 10 парсек (или на 32 световых года от Земли), почему 10? Просто удобно считать.
Таким образом, получаем, что абсолютная звёздная величина звезды - это видимая звёздная величина, при условии, что объект находится на расстоянии в 10 парсек от наблюдателя. Соответственно, зная видимую звёздную величину (которую мы выше нашли) и расстояние (с этим особых проблем нет, особенно, для звёзд в нашей Галактике), мы можем найти абсолютную звёздную величину! M = m - 5*lgd/d0, где M - абсолютная звёздная величина, m - видимая звёздная величина, lg - десятичный логарифм (или log10), d - расстояние до звезды в парсеках, а d0 - это то самое расстояние в 10 парсек, на которые мы мысленно удаляем звёзды.
Соответственно, все правила для величин сохраняются, например, яркость звезды +1m абсолютной звёздной величины больше в 2,512 раз звезды +2m... Но, теперь мы можем считать абсолютные звёздные величины для удалённых объектов, например, для квазаров - они будут в районе -25m, что примерно по яркости как Солнце. Только представьте, если бы квазар оказался от вас на расстоянии в 32 световых года (до ближайшей к нам звезды, не Солнца, а Проксимы Центавра 4,24 световых года), то светил бы почти так же ярко как наше Солнце! Вот теперь мы понимаем масштабы квазаров. Для сравнения, расстояние в 32 световых года больше расстояния от Земли до Солнца (145 млн км) в 65000 раз! Теперь, если мы Млечный Путь (весь) представим на расстоянии в 10 парсек - это сделать сложно, т.к. размеры Млечного Пути в тысячи раз больше, поэтому мы сожмём его (опять же мысленно) до размеров звёзды или точечного источника, и тогда его абсолютная звёздная величина будет в районе -20,5, что примерно в 100 раз тусклее квазара на том же расстоянии.
Теперь мы понимаем, насколько мощные эти квазары! Что же касается звёзд, то разброс абсолютных звёздных величин звёзд примерно от -10 до +17, наше Солнце занимает скромное место среди них с абсолютной звёздной величиной в +4,83m, т.е. если мы удалим Солнце в 65000 раз дальше (на 10 парсек) от Земли, оно станет очень тусклой звёздой, еле видимой невооружённым глазом в сельской местности... Поэтому, не удаляйте Солнце так далеко, это опасно! Бетельгейзе - знаменитый сверхгигант - будет светить ярче Венеры на таком расстоянии, его величина будет равна -5,6m. Теперь мы можем представить себе реальные яркости, благодаря вот такой нехитрой математике. Замечу, что для тел Солнечной Системы и для метеоров определение звёздных величин немного иное, но общая логика сохраняется.
Думаю, тут требуется пример того, зачем нам вообще знать абсолютные величины... Сразу можно догадаться, если у нас нет зависимости от расстояния, то влиять на яркость могут только размер звезды, температура её поверхности и другие факторы, например, пятна... Попробуем посчитать визуальную абсолютную звёздную величину, я не случайно сказал, "визуальную", ведь мы могли бы измерять звёздную величину с помощью ПЗС-матрицы или с помощью плёнки... Нас пока интересует наблюдения невооружённым глазом или через телескоп без применения техники для захвата изображения.
Пример для звезды Вега:
Примем визуальную видимую звёздную величину Веги как mv (где индекс v - означает visual) = +0,03m, тогда абсолютная (визуальная) звёздная величина Веги будет равна: 0,03 + 5(lg0,130 + 1) = +0.6m. Как вы заметили, мы употребили немного другую формулу, m + 5(lgp + 1), где p - это годичный звёздный параллакс, он считается довольно-таки просто (при условии, что сам параллакс мал и синус угла равен самому углу), обозначается буквой p или (греческой pi) и равен 1/d(в парсеках) = 1/7,68 (парсек до Веги) = 0,130'', общая формула sinp = a/r, где a - расстояние между Землёй и Солнцем, а r - расстояние между Землёй и звездой. Из малости угла формула превращается в p = 1/r, где r - расстояние в парсеках).
Измеряется параллакс в угловых секундах (для это удобно). Что означает эта величина в 0,130 угловой секунды (напомню, человеческий глаз может видеть вещи не менее 1 угловой минуты), т.е. это в сотни раз меньше, чем может различить наш глаз! Так вот, этот угловой размер в 0,130 угловой секунды равен угловому смещению звезды Вега относительно наблюдателя на Земле за полгода (при обращении Земли вокруг Солнца), за полгода Земля перемещается в противоположную точку орбиты и Вега начинает наблюдаться немного под другим углом, это всем известный параллакс, такой можно увидеть на iPhone или на некоторых сайтах, когда относительно движения мыши смещается фон и кажется, что всё движется... Так вот, указателем мыши в нашем случае выступает планета Земля, перемещение указателя мыши - движение Земли по орбите за полгода, а смещение фона - это смещение угла зрения на Вегу, этот угол в нашем случае меняется всего на 0,130 угловой секунды. Вот этот угол p - как раз и есть параллакс.
Пример: если мы видим звезду, на расстоянии в 1 парсек, с Земли, то её годичный параллакс равен одной угловой секунде. Парсек является одной из основных единиц измерения расстояний во Вселенной. Величина парсека определяется величиной астрономической единицы.
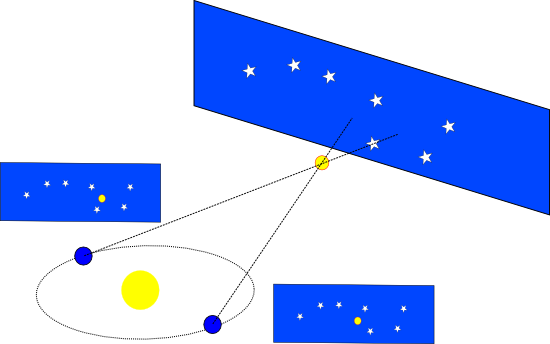
На рисунке: жёлтое - Солнце, синяя - Земля, движется по орбите вокруг Солнца, 1 Parsec - это 1 парсек - расстояние до звезды от Земли. Розовое - звезда, параллакс которой нам надо найти, и с которой расстояние от Земли до Солнца видно под углом 1 угловая секунда (это и есть её параллакс, т.к. звезда удалена на расстояние в 1 парсек), где угол p - и будет параллаксом, нам известно расстояние до ближайшей звезды, расстояние от Земли до Солнца, угол мы сможем найти без проблем из школьной тригонометрии. Движение этой звезды (розовой) будет выглядеть на фоне удалённых звёзд (distant stars) для нас на Земле как смещение относительно их на какое-то расстояние или изменение видимого положения объекта (apparent parallax motion of near star).
Теперь мы многое знаем о звёздных величинах, об абсолютных звёздных величинах, умеем их находить, делать выводы из вычислений, но до сих пор не знаем, зачем астрономам эти абсолютные звёздные величины нужны в быту, т.с.
Удалив все звёзды на равное расстояние, мы можем их сравнить! Например, если мы сравним звёзды с Солнцем, то получим много информации, т.к. о Солнце нам известно очень многое, в т.ч. его размеры, температура поверхности, масса и т.п. характеристики. Соответственно, практически пропорционально этих характеристики могут меняться и у других звёзд, в зависимости от их абсолютной звёздной величины...
Например, мы хотим найти массу звезды, зная её абсолютную звёздную величину, которую мы нашли из видимой звёздной величины и знания расстояния до звёзд или их параллакс (расстояние мы можем определить по параллаксу, о котором мы также узнали выше). Чтобы найти массу звезды, нам надо знать:
1) абсолютную звёздную величину звезды
2) массу Солнца
μ (масса звезды) / M(солнца) = 3,89 · 10^(−0,1194) · M(абс. зв. вел. звезды)
Давайте попробуем найти массу звезды Вега, и сравним с данными из Википедии.
μ = 3,89 · 10^(−0,1194) · M(абс.зв. вел. зв.) · M(масса солнца) = 3,89 · 10^(−0,1194) · 0,6 = 1,77 масс Солнца, из Вики мы видим, что мы ошиблись всего лишь на 0,2 массы Солнца. Не так уж и плохо!
Продолжение следует...